12 Regression with Qualitative Independent Variables
In this chapter, I will walk you through some analysis I conduct with an example dataset, in order to show how regression works with qualitative independent variables. I could have easily completed this analysis using the methods from Chapter 8, but it is important to see how regression can also be used as a method for comparing means across groups.
Let’s say I’m interested in studying how personality relates to gender. The most common model of personality in psychology is called the “Big Five.” One common measure consists of 50 survey items (the IPIP Big-Five Factor Markers), with 10 items for each of the five personality traits from the model.1 Figure 12.1 shows some of these questions and how they are formatted.

For now, I decide to focus on whether people are introverted or extroverted. Extroverts are outgoing and tend to enjoy interacting with others. Extroverts will tend to agree with the statement “I am the life of the party” while introverts will tend to agree with the item “I don’t talk a lot.”
I find a dataset that contains lots of responses to the Big Five personality questions as well as information on the gender of each respondent.2 There are 10 different questions related to extraversion, and the dataset has one variable for each of these 10 questions (Figure 12.2). The variable labeled e1 shows responses to the item “I am the life of the party.” A value of 1 means the respondent disagrees with this statement, while a 3 indicates neutral, and a 5 means they agree.
For all of the odd-numbered extraversion questions (e1, e3, e5, etc.), agreement indicates extraversion. For the even-numbered items (e2, e4, e6, etc.), agreement indicates introversion. To create a single extraversion variable that combines responses from all 10 survey items, I create a tally, adding up all the values for odd-numbered questions and then subtracting the responses to the even-numbered questions. An extreme extrovert will have a 5 for all the odd-numbered questions and a 1 for all of the even-numbered ones, giving them a score of 20 (\(5 \times 5-5 \times 1=20\)). An extreme introvert will have a -20 since they will answer 1 to all the odd-numbered questions and 5 to all the even-numbered ones (\(5 \times 1-5 \times 5=-20\)).
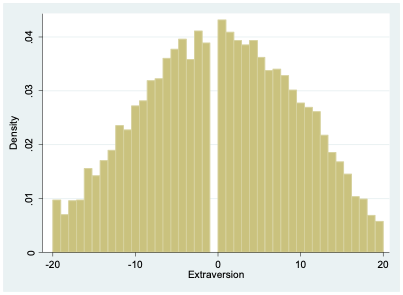
As Figure 12.3 indicates, most people lie somewhere in the middle between introversion and extraversion.
Our gender variable was measured by asking respondents “What is your gender?” and they could choose from male (coded as a 1), female (2), or other (3). In a moment, we’ll consider those who responded “other,” but for now, let’s just look at those who chose either male or female.
12.1 Predicting extraversion using gender
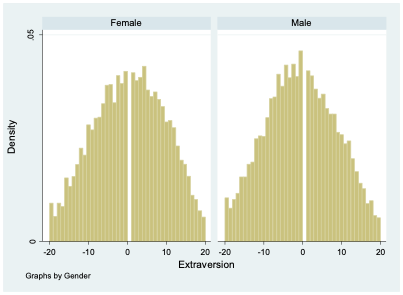
If I want to describe differences in extraversion by gender in this dataset, I can compute the mean value of extraversion for males and for females. It turns out that males have an average extraversion of -0.46 while females’ average level of extraversion is 0.53. Thus, the average female is about 1-point more extroverted than the average male. But of course, there is abundant variation in extraversion among both groups, as seen clearly in Figure 12.4. There are plenty of females who are introverts and plenty of males who are extroverts.
If you asked me to guess the extraversion level of someone in this dataset and the only thing you told me about them was their gender, my best bet would probably be to guess the average extraversion level for someone of that gender. So for a female I knew nothing else about, I would guess their extraversion to be 0.53, while for a male I’d guess -0.46.
When we’re working with data, sometimes it’s helpful to express how I would make a guess about a dependent variable (extraversion) based on an independent variable (gender) using a mathematical formula. In fact, this is exactly what we do when we run a regression. There are many ways I could write this formula, but I’ll show just two for now. First, I could write:
\[ \widehat{Extraversion}=0.53 \times Female-0.46 \times Male \tag{12.1}\]
Notice I’ve added a “hat” above the name of the variable Extraversion; this hat means that I’m making a guess about the value of that variable (I’m guessing the level of extraversion based on gender). The equation has two other variables Female and Male, and these two variables will take on a value of 1 if the person’s gender is equal to the name of the variable and will otherwise take on a value of 0. For a female, Female will equal 1 and Male will equal 0, giving us:
\[ \widehat{Extraversion}=0.53 \times (1)-0.46 \times (0)=0.53 \]
So our guess for the level of extraversion (\(\widehat{Extraversion}\)) of a female we know nothing about is 0.53.
For a male, our guess is:
\[ \widehat{Extraversion}=0.53 \times (0)-0.46 \times (1)=-0.46 \]
There’s a second way I can write my formula, which will turn out to be more useful in the future when we come to consider multiple factors at the same time that might help us predict the value of a dependent variable. Rather than having two variables to represent gender in my equation, I can just use one:
\[ \widehat{Extraversion}=0.53-0.99 \times Male \tag{12.2}\]
In Equation 12.2, we start from female as our baseline. Notice that the first number we see (0.53) is our guess for the value of extraversion for a female. When we’re considering a female, Male=0, so:
\[ \widehat{Extraversion}=0.53-0.99 \times 0=0.53 \]
Thus, we get the right prediction for females from this equation, even though we didn’t include a variable specifically for females. If we have a male, Male=1, so we get:
\[ \widehat{Extraversion}=0.53-0.99 \times 1=-0.46 \]
This is the same prediction we got before. Remember, I decided to initially just analyze respondents who selected either male or female. Since we are only considering two categories (male or female), and each respondent is either a male or a female, saying Male = 1 lets me know that Female = 0. It’s actually repetitive in this context to both say that Male = 1 and Female = 0. Similarly, saying Male = 0 implies that Female = 1. So I can simplify my equation by just including one variable to indicate binary gender.
Notice that in Equation 12.2, the number next to Male is equal to the difference between the average level of extraversion for females and the average level for males (0.53-(-0.46)=0.99). This is because Equation 12.2 starts with females as the baseline, so to get our prediction for males, we have to adjust our baseline prediction by the average difference for males.
Equation 12.2 is also typically how we will arrange our equation when we’re running a regression.
12.2 Prediction with more than two categories for gender
I now move beyond the gender binary and consider the “other” category in survey responses. The average level of extraversion among those identifying as neither male nor female is -5.66. This is notably more introverted (on average) than those who identify as male or female. As with males and females, there is still considerable variation among those identifying as “other” gender (Figure 12.5).
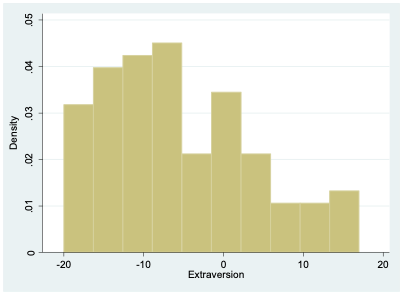
The number of respondents selecting “other” is relatively small (102), so it’s not terribly surprising that this histogram looks a bit choppier than the ones we saw before.
Again, if we had to make a guess about the level of extraversion of someone, and all we knew about that person was that their gender is other, we would probably want to guess the mean value among other-gender respondents (-5.66). Modifying Equation 12.1 to incorporate a third category is relatively straightforward:
\[ \widehat{Extraversion}=0.53 \times Female-0.46 \times Male-5.69 \times Other \tag{12.3}\]
For someone who identifies as female, we would plug in Female = 1, Male = 0, and Other = 0:
\[ \widehat{Extraversion}=0.53 \times (1)-0.46 \times (0)-5.66 \times (0)=0.53 \]
If someone identifies as other-gender, we would use Female = 0, Male = 0, and Other = 1:
\[ \widehat{Extraversion}=0.53 \times (0)-0.46 \times (0)-5.66 \times (1)=-5.66 \]
We can also return to the format of Equation 12.2 but modify it to include the other category. This is how we will typically write our equation if we are doing a regression:
\[ \widehat{Extraversion}=0.53-0.99 \times Male-6.19 \times Other \tag{12.4}\]
Now that there are three possible values for gender (female, male, and other), knowing the value of Male doesn’t necessarily allow us to conclude what the value of female is. If Male = 0, the individual could identify as either female or other. So we have to include a second variable. In this case, we chose to include the variable Other. If we know the values of Male and Other, we can always figure out the value of Female by process of elimination.
For an other-gender person, we plug in Male = 0, and Other = 1:
\[ \widehat{Extraversion}=0.53-0.99 \times (0)-6.19 \times (1)=-5.66 \]
When considering a female, we use Male = 0, and Other = 0:
\[ \widehat{Extraversion}=0.53-0.99 \times (0)-6.19 \times (0)=0.53 \]
Equation 12.3 and Equation 12.4 indicate equivalent predictions for extraversion based on gender; they just offer this information in two different formats. Equation 12.4 might be a bit trickier to understand for now, but it will become very useful in the future.
Notice that we can talk about gender either as one qualitative variable with three possible values (female, male, or other), or we can talk about it as a series of three variables (Female, Male, and Other) that can each take on a value of either 0 or 1 (we call such variables “binary” or “dummy” variables). This can make things a bit confusing, but the important thing to remember is that when we have a qualitative variable with more than two categories, we’ll need to break out the categories into a set of dummy variables for purposes of representing the qualitative variable in an equation.
However, as Equation 12.2 and Equation 12.4 illustrate, we don’t necessarily need a dummy variable for every single category. Specifically, whenever we want to create an equation with a qualitative independent variable in a format like Equation 12.2 or Equation 12.4, the number of dummy variables should be equal to the number of categories minus one. Since our gender variable can take on three possible values in this example, we included two independent variables in Equation 12.4. No dummy variable is included for female, so we call female the omitted category, also known as the reference group or baseline category. Remember, the first number in Equation 12.4 is 0.53, which represents our guess for females—the baseline category. If we instead had a qualitative variable with five categories, we would include four dummy variables in our equation.
As we will see at the end of the next chapter, it doesn’t really matter which group we select as the omitted category because we get equivalent predictions regardless of which one we choose.
Goldberg, L. R. (1992). The development of markers for the Big-Five factor structure. Psychological assessment, 4(1), 26.↩︎
https://openpsychometrics.org/_rawdata/ (the file I used is called “BIG5.zip”)↩︎