9  Comparing Groups (How Two Qualitative Variables Relate to One Another)

We previously learned how to graphically depict the relationship between two qualitative variables with a bar chart (Section 1.3.3.1). To make a comparison that includes a significance test, we will need to use the chi square distribution, together with a contingency table.

9.1 Chi Square Distribution1

While the details of the Chi Square distribution are not so important for understanding how to interpret a test of the relationship between two qualitative variable, a brief explanation is nonetheless provided here (with more information provided in this chapter’s appendix). A standard normal deviate is a random sample from the standard normal distribution. The Chi Square distribution is the distribution of the sum of squared standard normal deviates, and the degrees of freedom of the distribution is equal to the number of standard normal deviates being summed. Again, don’t worry if you don’t follow these details since they are not important for the average reader of this text.

Chi Square distributions are positively skewed, but as the degrees of freedom increases, the degree of skew decreases and the Chi Square distribution approaches a normal distribution. Figure 9.1 shows density functions for three Chi Square distributions. Notice how the skew decreases as the degrees of freedom increases.

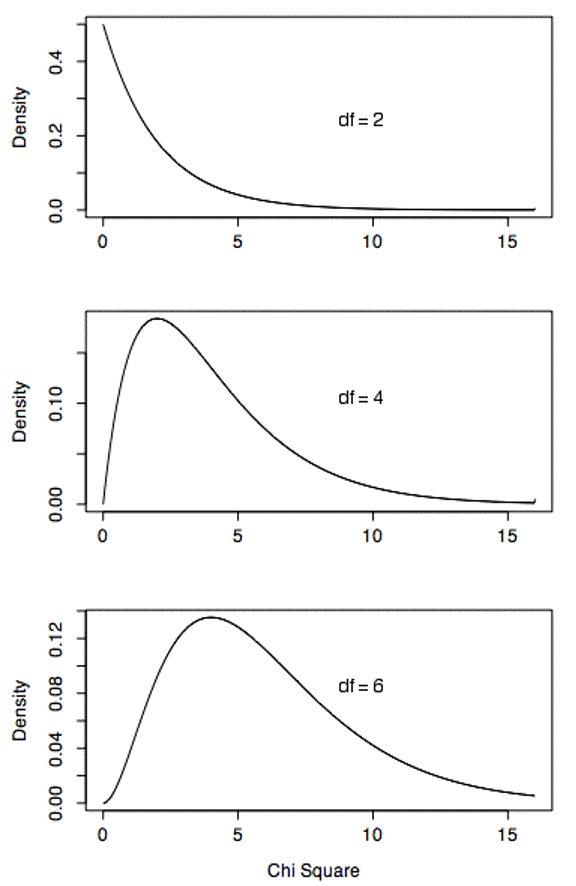
Figure 9.1: Chi Square distributions with 2, 4, and 6 degrees of freedom.

The Chi Square distribution is very important because many test statistics are approximately distributed as Chi Square. Two of the more common tests using the Chi Square distribution are tests of deviations of differences between theoretically expected and observed frequencies (one-way tables) and the relationship between qualitative variables (contingency tables). Numerous other tests beyond the scope of this work are based on the Chi Square distribution.

9.2 One-Way Tables2

The Chi Square distribution can be used to test whether observed data differ significantly from theoretical expectations. For example, for a fair six-sided die, the probability of any given outcome on a single roll would be 1/6. The data in Table 9.1 were obtained by rolling a six-sided die 36 times. However, as can be seen in Table 9.1, some outcomes occurred more frequently than others. For example, a “3” came up nine times, whereas a “4” came up only two times. Are these data consistent with the hypothesis that the die is a fair die? Naturally, we do not expect the sample frequencies of the six possible outcomes to be the same since chance differences will occur. So, the finding that the frequencies differ does not mean that the die is not fair. One way to test whether the die is fair is to conduct a significance (hypothesis) test. The null hypothesis is that the die is fair. This hypothesis is tested by computing the probability of obtaining frequencies as discrepant or more discrepant from a uniform distribution of frequencies as obtained in the sample. If this probability is sufficiently low, then the null hypothesis that the die is fair can be rejected.

Table 9.1: Outcome Frequencies from a Six-Sided Die.
Outcome Frequency
1 8
2 5
3 9
4 2
5 7
6 5

The first step in conducting the significance test is to compute the expected frequency for each outcome given that the null hypothesis is true. For example, the expected frequency of a “1” is 6 since the probability of a “1” coming up is 1/6 and there were a total of 36 rolls of the die.

Expected frequency = (1/6)(36) = 6

Note that the expected frequencies are expected only in a theoretical sense. We do not really “expect” the observed frequencies to match the “expected frequencies” exactly.

The calculation continues as follows. Letting E be the expected frequency of an outcome and O be the observed frequency of that outcome, compute

\[ \frac{(E-O)^2}{E} \]

for each outcome. Table 9.2 shows these calculations.

Table 9.2: Outcome Frequencies from a Six-Sided Die.
Outcome E O \(\frac{(E-O)^2}{E}\)
1 6 8 0.667
2 6 5 0.167
3 6 9 1.500
4 6 2 2.667
5 6 7 0.167
6 6 5 0.167

Next we add up all the values in Column 4 of Table 9.2.

\[ \sum{\frac{(E-O)^2}{E}}=5.333 \]

This sampling distribution of

\[ \sum{\frac{(E-O)^2}{E}} \]

is approximately distributed as Chi Square with k-1 degrees of freedom, where k is the number of categories (in our example, the six possible values we might get from a die roll). Therefore, for this problem the test statistic is

\[ \chi^2_5=5.333 \]

which means the value of Chi Square with 5 degrees of freedom is 5.333.

From a Chi Square calculator3 it can be determined that the probability of a Chi Square of 5.333 or larger is 0.377. Therefore, the null hypothesis that the die is fair cannot be rejected.

This Chi Square test can also be used to test other deviations between expected and observed frequencies. The following example shows a test of whether the variable “University GPA” in the “SAT and College GPA” case study4 (used previously to demonstrate regression) is normally distributed.

The first column in Table 9.3 shows the standard normal distribution divided into four ranges. The second column shows the proportions of a standard normal distribution falling in the ranges specified in the first column. For example, we see that for the range 0 to 1, the proportion is 0.341 (or 34.1%). This follows directly from what we learned in Chapter 5; 68% of the area under the standard normal distribution lies between -1 and 1, so naturally 34% (half of 68%) will be covered by [0, 1]. The expected frequencies (E) are calculated by multiplying the number of scores (105) by the proportion expected according to the standard normal distribution. The final column shows the observed number of scores (O) in each range, after standardizing the University GPA variable so that it will map onto the standard normal distribution (see Section 5.2.3). It is clear from the table that the observed frequencies vary greatly from the expected frequencies. Note that if the distribution were normal, we would expect only about 35 scores between 0 and 1, whereas 60 were observed.

Table 9.3: Expected and Observed Scores for 105 University GPA Scores.
Range Proportion E O
Above 1 0.159 16.695 9
0 to 1 0.341 35.805 60
-1 to 0 0.341 35.805 17
Below -1 0.159 16.695 19

The test of whether the observed scores deviate significantly from the expected scores is computed using the familiar calculation.

\[ \chi^2_3=\sum\frac{(E-O)^2}{E}=30.09 \]

The subscript “3” means there are three degrees of freedom. As before, the degrees of freedom is the number of outcomes (in our example, the number of ranges listed in Table 9.3) minus 1, which is 4 - 1 = 3 in this example. A Chi Square distribution calculator shows that p < 0.001 for this Chi Square. Therefore, the null hypothesis that the scores are normally distributed can be rejected.

9.3 Contingency Tables5

This section shows how to use Chi Square to test the relationship between qualitative variables for significance. For example, Table 9.4 shows the data from the Mediterranean Diet and Health case study,6 in which 605 survivors of a heart attack were randomly assigned to follow either (1) a low-fat diet similar to one recommended at the time by the American Heart Association (AHA) or (2) a Mediterranean-type diet rich in vegetables, fruits, and grains.

Table 9.4: Frequencies for Diet and Health Study.
Outcome Total
Diet Cancers Fatal Heart Disease Non-Fatal Heart Disease Healthy
AHA 15 24 25 239 303
Mediterranean 7 14 8 273 302
Total 22 38 33 512 605

The question is whether there is a significant relationship between diet and outcome. Again, software can calculate a p-value for us in order to test for significance. But if we are wondering what’s going on under the hood, the first step is to compute the expected frequency for each cell based on the assumption that there is no relationship. These expected frequencies are computed from the totals as follows. We begin by computing the expected frequency for the AHA Diet/Cancers combination. Note that 22/605 subjects developed cancer. The proportion who developed cancer is therefore 0.0364. If there were no relationship between diet and outcome, then we would expect 0.0364 of those on the AHA diet to develop cancer. Since 303 subjects were on the AHA diet, we would expect (0.0364)(303) = 11.02 cancers on the AHA diet. Similarly, we would expect (0.0364)(302) = 10.98 cancers on the Mediterranean diet. In general, the expected frequency for a cell in the \(i\)th row and the \(j\)th column is equal to

\[ E_{ij}=\frac{T_iT_j}{T} \]

where \(E_{ij}\) is the expected frequency for cell \(i,j\), \(T_i\) is the total for the \(i\)th row, \(T_j\) is the total for the \(j\)th column, and \(T\) is the total number of observations. For the AHA Diet/Cancers cell, \(i = 1\), \(j = 1\), \(T_i = 303\), \(T_j = 22\), and \(T = 605\). Table 9.5 shows the expected frequencies (in parenthesis) for each cell in the experiment.

The significance test is conducted by computing Chi Square as follows.

\[ \chi^2_3=\sum\frac{(E-O)^2}{E}=-16.55 \]

The degrees of freedom is equal to \((r-1)(c-1)\), where \(r\) is the number of rows and \(c\) is the number of columns. For this example, the degrees of freedom is \((2-1)(4-1) = 3\). The Chi Square calculator7 can be used to determine that the probability value for a Chi Square of 16.55 with three degrees of freedom is equal to 0.0009. Therefore, the null hypothesis of no relationship between diet and outcome can be rejected.

Table 9.5: Observed and Expected Frequencies for Diet and Health Study.
Outcome
Diet Cancers Fatal Heart Disease Non-Fatal Heart Disease Healthy
AHA 15
(11.02)		 24
(19.03)		 25
(16.53)		 239
(256.42)
Mediterranean 7
(10.98)		 14
(18.97)		 8
(16.47)		 273
(255.58)
Total 22 38 33 512

9.3.1 Drawing Substantive Conclusions from a Contingency Table8

Now that we know there is a statistically significant relationship between diet and health outcome (since we rejected the null hypothesis of no relationship), we will naturally wonder what kind of relationship exists. Specifically, which diet is associated with better health? To answer this, we must look to the specific values within the cells and describe the patterns we observe. One straightforward way to do this is to make note of where the observed frequency differs notably from the expected frequency.

From Table 9.5, we can see that for those on the AHA diet, the frequencies for cancers, fatal heart disease, and non-fatal heart disease are all higher than expected. At the same time, the frequency for “healthy” is lower than expected on the AHA diet. Results for the Mediterranean diet are the exact opposite: cancers and both types of heart disease occur less frequently than expected, and the healthy outcome occurs more than expected. Thus, the Mediterranean diet is unambiguously associated with better outcomes than the AHA diet.

Though it is easy to make sense of results in this manner based on a comparison of observe to expected frequencies, the typical contingency table you encounter will probably not display expected frequencies. Instead, it is common to include percentages by row or by column, which can also be used to draw conclusions about the nature of a relationship between variables. For example, in Table 9.6, the expected frequencies from the prior table have been replaced by percentages. The percentages shown in this table are calculated by row, meaning that they are found by dividing the frequency in each cell by the total for that row, shown in the final column.

Table 9.6: Frequencies and Percentages by Row for Diet and Health Study.
Outcome Total
Diet Cancers Fatal Heart Disease Non-Fatal Heart Disease Healthy
AHA 15
4.95%		 24
7.92%		 25
8.25%		 239
78.88%		 303
100%
Mediterranean 7
2.32%		 14
4.64%		 8
2.65%		 273
90.40%		 302
100%
Total 22
3.64%		 38
6.28%		 33
5.45%		 512
84.63%		 605
100%

Drawing conclusions based on column or row percentages takes some care, and it is easy to make mistakes if you are not careful. For example, consider the AHA/Cancers cell, which shows 4.95%. Because this seems like a small percentage, it is tempting to conclude that being on the AHA diet is not associated with having cancer. However, that conclusion would be wrong. Since the percentages have been calculated by row, the key to finding meaningful patterns will be to compare across the percentages found within the same column. In this case, we see that the 4.95% in the AHA-Cancers cell is over twice as large as the 2.32% shown in the Mediterranean/Cancers cell right below it. To make sense of these percentages, remember that we have calculated percentages by row, meaning that the frequency in the cell is divided by the total at the far right of the table. So the 4.95% means that among all those on the AHA diet (303 individuals in total), 4.95% have cancer. By comparison, only around 2% (2.32% to be precise) of those on a Mediterranean diet have cancer. Both percentages are small, because cancer is (fortunately) a relatively rare outcome; at the bottom of the table we see that only 3.64% of participants overall have cancer. Still, since the percentage is higher among those on the AHA diet than on the Mediterranean diet, we can say that the AHA diet is positively associated with having cancer.

If we continue moving down the table column by column, we see that rates of heart disease are higher among those on the AHA diet (7.92% for fatal and 8.25% for non-fatal) than among those on the Mediterranean diet (4.64% and 2.65%). Finally, around 90% of those on the Mediterranean diet are healthy, while just under 79% of those on the AHA diet are.

We can reach an equivalent conclusion by examining percentages that are calculated by column, as shown in Table 9.7. Here, percentages are calculated by dividing the frequency in each cell by the total shown at the bottom of the column.

Table 9.7: Frequencies and Percentages by Column for Diet and Health Study.
Outcome Total
Diet Cancers Fatal Heart Disease Non-Fatal Heart Disease Healthy
AHA 15
68.18%		 24
63.16%		 25
75.76%		 239
46.68%		 303
50.08%
Mediterranean 7
31.82%		 14
36.84%		 8
24.24%		 273
53.32%		 302
49.92%
Total 22
100%		 38
100%		 33
100%		 512
100%		 605
100%

The AHA/Cancers cell shows 68.18%, indicating that around 68% of those who have cancer are on the AHA diet. In the case of this particular dataset, the split of participants between the two diets is approximately 50-50 (as shown by the percentages in the final column), so finding that the percentage of those with cancer who are on the AHA diet is well above 50% actually does indicate that individuals on the AHA diet are overrepresented among those with cancer. But remember, you cannot generally assume that 50% is a reasonable baseline for comparison; if, for example, 80% of study participants were on the AHA diet, seeing any percentage smaller than 80% for the AHA-Cancers would indicate that those on the AHA diet were underrepresented among those with cancer.

As a general rule, when percentages are calculated by columns, the key to finding meaningful patterns is making comparisons across the columns (within the same row), such as noticing that the 68.18% in the AHA-Cancers cell is greater than the 50.08% in the AHA Total cell. One can also see that while people on the AHA diet make up a clear majority of those with heart disease (both fatal and non-fatal), among those who are healthy only around 47% are on the AHA diet. As a clear contrast, those on the Mediterranean diet make up around 53% of the healthy subjects but just 32% of those with cancer, 37% of those with fatal heart disease, and 24% of those with non-fatal heart disease. Thus, we see consistent indication that outcomes are better for subjects on the Mediterranean diet, as opposed to the AHA one.

As you can now see, regardless of whether we examine (1) expected versus observed outcomes, (2) percentages by row, or (3) percentages by column, we reach the same conclusion: health outcomes are uniformly better for those on the Mediterranean diet. All three approaches are equally valid ways of evaluating associations from a contingency table, and you normally need use only one. We examined all three here for illustrative purposes since each approach is one you may encounter in your own analysis or in a research report.

9.3.2 Key Assumption of the Chi Square Test

A key assumption of this Chi Square test is that each subject contributes data to only one cell. Therefore, the sum of all cell frequencies in the table must be the same as the number of subjects in the experiment. Consider an experiment in which each of 16 subjects attempted two anagram problems. The data are shown in Table 9.8.

Table 9.8: Anagram Problem Data.
Anagram 1 Anagram 2
Solved 10 4
Did not Solve 6 12

It would not be valid to use the Chi Square test on these data since each subject contributed data to two cells: one cell based on their performance on Anagram 1 and one cell based on their performance on Anagram 2. The total of the cell frequencies in the table is 32, but the total number of subjects is only 16.

Chapter 9 Appendix: More about the Chi Square Distribution9

As noted in the main text, the degrees of freedom of the distribution is equal to the number of standard normal deviates being summed. Therefore, Chi Square with one degree of freedom, written as \(\chi^2(1)\), is simply the distribution of a single normal deviate squared. The area of the \(\chi^2(1)\) distribution below 4 is the same as the area of a standard normal distribution below 2, since 4 is 22.

Consider the following problem: you sample two scores from a standard normal distribution, square each score, and sum the squares. What is the probability that the sum of these two squares will be six or higher? Since two scores are sampled, the answer can be found using the Chi Square distribution with two degrees of freedom. A Chi Square calculator can be used to find that the probability of a Chi Square (with 2 df) being six or higher is 0.050.

The mean of a Chi Square distribution is its degrees of freedom.

  1. This section is adapted from David M. Lane. “Chi Square Distribution.” Online Statistics Education: A Multimedia Course of Study. https://onlinestatbook.com/2/chi_square/distribution.html↩︎

  2. This section is adapted from David M. Lane. “One-Way Tables (Testing Goodness of Fit).” Online Statistics Education: A Multimedia Course of Study. https://onlinestatbook.com/2/chi_square/one-way.html↩︎

  3. https://onlinestatbook.com/2/calculators/chi_square_prob.html↩︎

  4. https://onlinestatbook.com/2/case_studies/sat.html↩︎

  5. This section is adapted from David M. Lane. “Contingency Tables.” Online Statistics Education: A Multimedia Course of Study. https://onlinestatbook.com/2/chi_square/contingency.html↩︎

  6. https://onlinestatbook.com/2/case_studies/diet.html↩︎

  7. https://onlinestatbook.com/2/calculators/chi_square_prob.html↩︎

  8. This subsection is written by Nathan Favero.↩︎

  9. This section is adapted from David M. Lane. “Chi Square Distribution.” Online Statistics Education: A Multimedia Course of Study. https://onlinestatbook.com/2/chi_square/distribution.html↩︎