4 Estimation
4.1 Populations and Samples1
In statistics, we often rely on a sample — that is, a small subset of a larger set of data — to draw inferences about the larger set. The larger set is known as the population from which the sample is drawn.
Example #1: You have been hired by the National Election Commission to examine how the American people feel about the fairness of the voting procedures in the U.S. Whom will you ask?
It is not practical to ask every single American how he or she feels about the fairness of the voting procedures. Instead, we query a relatively small number of Americans, and draw inferences about the entire country from their responses. The Americans actually queried constitute our sample of the larger population of all Americans. The mathematical procedures whereby we convert information about the sample into intelligent guesses about the population fall under the rubric of inferential statistics.
A sample is typically a small subset of the population. In the case of voting attitudes, we would sample a few thousand Americans drawn from the hundreds of millions that make up the country. In choosing a sample, it is therefore crucial that it not over-represent one kind of citizen at the expense of others. For example, something would be wrong with our sample if it happened to be made up entirely of Florida residents. If the sample held only Floridians, it could not be used to infer the attitudes of other Americans. The same problem would arise if the sample were comprised only of Republicans. Inferential statistics are based on the assumption that sampling is random. We trust a random sample to represent different segments of society in close to the appropriate proportions (provided the sample is large enough; see below).
Example #2: We are interested in examining how many math classes have been taken on average by current graduating seniors at American colleges and universities during their four years in school. Whereas our population in the last example included all US citizens, now it involves just the graduating seniors throughout the country. This is still a large set since there are thousands of colleges and universities, each enrolling many students. (New York University, for example, enrolls 48,000 students.) It would be prohibitively costly to examine the transcript of every college senior. We therefore take a sample of college seniors and then make inferences to the entire population based on what we find. To make the sample, we might first choose some public and private colleges and universities across the United States. Then we might sample 50 students from each of these institutions. Suppose that the average number of math classes taken by the people in our sample were 3.2. Then we might speculate that 3.2 approximates the number we would find if we had the resources to examine every senior in the entire population. But we must be careful about the possibility that our sample is non-representative of the population. Perhaps we chose an overabundance of math majors, or chose too many technical institutions that have heavy math requirements. Such bad sampling makes our sample unrepresentative of the population of all seniors.
Example #3: A substitute teacher wants to know how students in the class did on their last test. The teacher asks the 10 students sitting in the front row to state their latest test score. He concludes from their report that the class did extremely well. What is the sample? What is the population? Can you identify any problems with choosing the sample in the way that the teacher did?
In Example #3, the population consists of all students in the class. The sample is made up of just the 10 students sitting in the front row. The sample is not likely to be representative of the population. Those who sit in the front row tend to be more interested in the class and tend to perform higher on tests. Hence, the sample may perform at a higher level than the population.
Example #4: A coach is interested in how many cartwheels the average college freshmen at his university can do. Eight volunteers from the freshman class step forward. After observing their performance, the coach concludes that college freshmen can do an average of 16 cartwheels in a row without stopping.
In Example #4, the population is the class of all freshmen at the coach’s university. The sample is composed of the 8 volunteers. The sample is poorly chosen because volunteers are more likely to be able to do cartwheels than the average freshman; people who can’t do cartwheels probably did not volunteer! In the example, we are also not told of the gender of the volunteers. Were they all women, for example? That might affect the outcome, contributing to the non-representative nature of the sample (if the school is co-ed).
4.1.1 Simple Random Sampling
Researchers adopt a variety of sampling strategies. The most straightforward is simple random sampling. Such sampling requires every member of the population to have an equal chance of being selected into the sample. In addition, the selection of one member must be independent of the selection of every other member. That is, picking one member from the population must not increase or decrease the probability of picking any other member (relative to the others). In this sense, we can say that simple random sampling chooses a sample by pure chance. To check your understanding of simple random sampling, consider the following example. What is the population? What is the sample? Was the sample picked by simple random sampling? Is it biased?
Example #5: A research scientist is interested in studying the experiences of twins raised together versus those raised apart. She obtains a list of twins from the National Twin Registry, and selects two subsets of individuals for her study. First, she chooses all those in the registry whose last name begins with Z. Then she turns to all those whose last name begins with B. Because there are so many names that start with B, however, our researcher decides to incorporate only every other name into her sample. Finally, she mails out a survey and compares characteristics of twins raised apart versus together.
In Example #5, the population consists of all twins recorded in the National Twin Registry. It is important that the researcher only make statistical generalizations to the twins on this list, not to all twins in the nation or world. That is, the National Twin Registry may not be representative of all twins. Even if inferences are limited to the Registry, a number of problems affect the sampling procedure we described. For instance, choosing only twins whose last names begin with Z does not give every individual an equal chance of being selected into the sample. Moreover, such a procedure risks over-representing ethnic groups with many surnames that begin with Z. There are other reasons why choosing just the Z’s may bias the sample. Perhaps such people are more patient than average because they often find themselves at the end of the line! The same problem occurs with choosing twins whose last name begins with B. An additional problem for the B’s is that the “every-other-one” procedure disallowed adjacent names on the B part of the list from being both selected. Just this defect alone means the sample was not formed through simple random sampling.
4.1.2 Sample size matters
Recall that the definition of a random sample is a sample in which every member of the population has an equal chance of being selected. This means that the sampling procedure rather than the results of the procedure define what it means for a sample to be random. Random samples, especially if the sample size is small, are not necessarily representative of the entire population. For example, if a random sample of 20 subjects were taken from a population with an equal number of males and females, there would be a nontrivial probability (0.06) that 70% or more of the sample would be female. Such a sample would not be representative, although it would be drawn randomly. Only a large sample size makes it likely that our sample is close to representative of the population. For this reason, inferential statistics take into account the sample size when generalizing results from samples to populations. In later chapters, you’ll see what kinds of mathematical techniques ensure this sensitivity to sample size.
4.1.3 More complex sampling
Sometimes it is not feasible to build a sample using simple random sampling. To see the problem, consider the fact that both Dallas and Houston are competing to be hosts of the 2012 Olympics. Imagine that you are hired to assess whether most Texans prefer Houston to Dallas as the host, or the reverse. Given the impracticality of obtaining the opinion of every single Texan, you must construct a sample of the Texas population. But now notice how difficult it would be to proceed by simple random sampling. For example, how will you contact those individuals who don’t vote and don’t have a phone? Even among people you find in the telephone book, how can you identify those who have just relocated to California (and had no reason to inform you of their move)? What do you do about the fact that since the beginning of the study, an additional 4,212 people took up residence in the state of Texas? As you can see, it is sometimes very difficult to develop a truly random procedure. For this reason, other kinds of sampling techniques have been devised. We now discuss two of them.
4.1.4 Random Assignment
In experimental research, populations are often hypothetical. For example, in an experiment comparing the effectiveness of a new anti-depressant drug with a placebo, there is no actual population of individuals taking the drug. In this case, a specified population of people with some degree of depression is defined and a random sample is taken from this population. The sample is then randomly divided into two groups; one group is assigned to the treatment condition (drug) and the other group is assigned to the control condition (placebo). This random division of the sample into two groups is called random assignment. Random assignment is critical for the validity of an experiment. For example, consider the bias that could be introduced if the first 20 subjects to show up at the experiment were assigned to the experimental group and the second 20 subjects were assigned to the control group. It is possible that subjects who show up late tend to be more depressed than those who show up early, thus making the experimental group less depressed than the control group even before the treatment was administered.
In experimental research of this kind, failure to assign subjects randomly to groups is generally more serious than having a non-random sample. Failure to randomize (the former error) invalidates the experimental findings. A non-random sample (the latter error) simply restricts the generalizability of the results.
4.1.5 Stratified Sampling
Since simple random sampling often does not ensure a representative sample, a sampling method called stratified random sampling is sometimes used to make the sample more representative of the population. This method can be used if the population has a number of distinct “strata” or groups. In stratified sampling, you first identify members of your sample who belong to each group. Then you randomly sample from each of those subgroups in such a way that the sizes of the subgroups in the sample are proportional to their sizes in the population.
Let’s take an example: Suppose you were interested in views of capital punishment at an urban university. You have the time and resources to interview 200 students. The student body is diverse with respect to age; many older people work during the day and enroll in night courses (average age is 39), while younger students generally enroll in day classes (average age of 19). It is possible that night students have different views about capital punishment than day students. If 70% of the students were day students, it makes sense to ensure that 70% of the sample consisted of day students. Thus, your sample of 200 students would consist of 140 day students and 60 night students. The proportion of day students in the sample and in the population (the entire university) would be the same. Inferences to the entire population of students at the university would therefore be more secure.
4.2 Confidence Intervals: A Key Tool for Estimation2
Say you were interested in the mean weight of 10-year-old girls living in the United States. Since it would have been impractical to weigh all the 10-year-old girls in the United States, you took a sample of 16 and found that the mean weight was 90 pounds. This sample mean of 90 is a point estimate of the population mean. A point estimate by itself is of limited usefulness because it does not reveal the uncertainty associated with the estimate; you do not have a good sense of how far this sample mean may be from the population mean. For example, can you be confident that the population mean is within 5 pounds of 90? You simply do not know.
Confidence intervals provide more information than point estimates. Confidence intervals for means are intervals constructed using a procedure that will contain the population mean a specified proportion of the time, typically either 95% or 99% of the time. These intervals are referred to as 95% and 99% confidence intervals respectively. An example of a 95% confidence interval is shown below:
\[ 72.85 < \mu < 107.15 \]
Based on this interval, there is good reason to believe that the population mean lies between these two bounds of 72.85 and 107.15 since 95% of the time confidence intervals contain the true mean.
If repeated samples were taken and the 95% confidence interval computed for each sample, 95% of the intervals would contain the population mean. Naturally, 5% of the intervals would not contain the population mean.
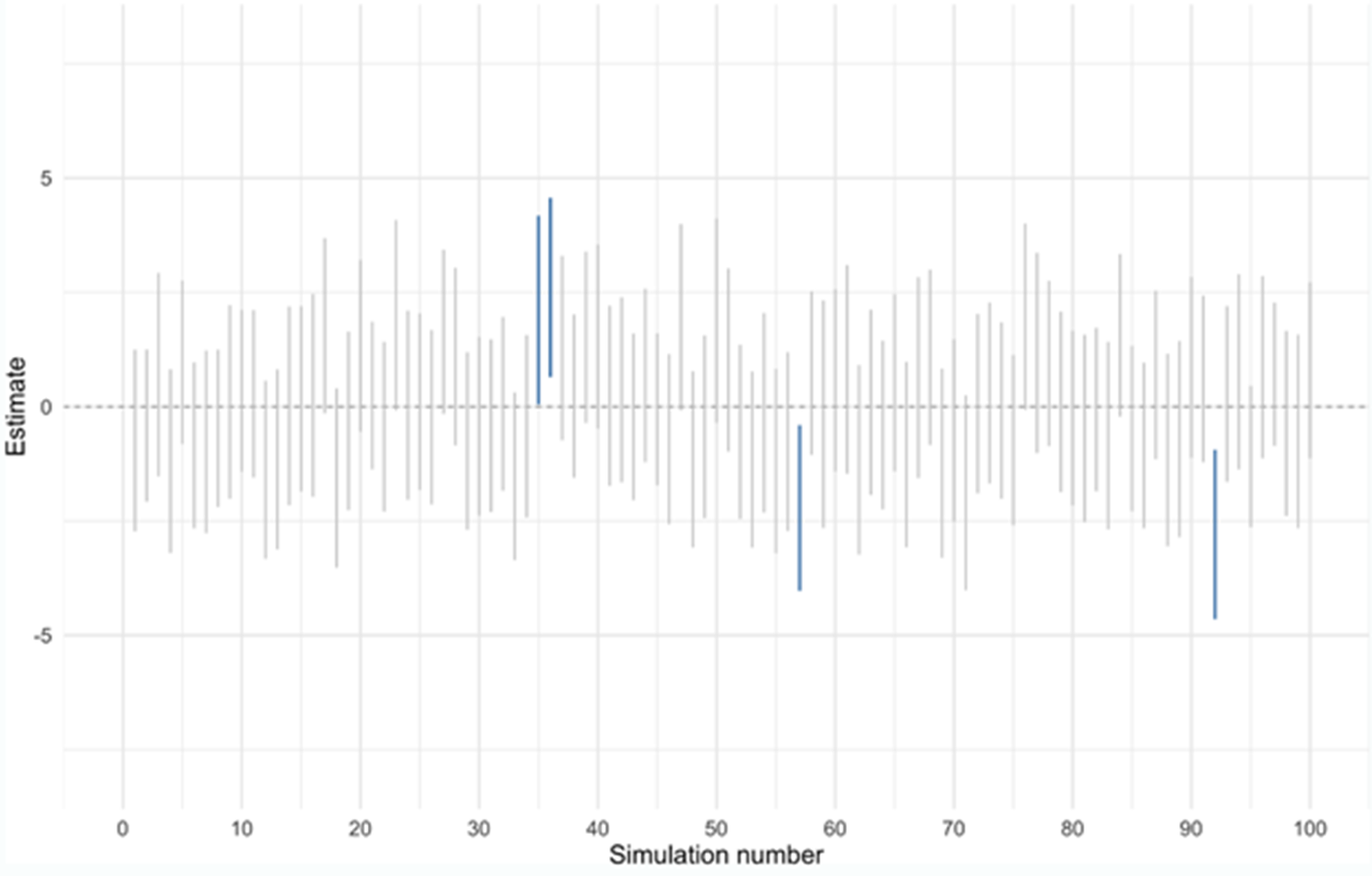
This property of 95% confidence intervals is demonstrated in Figure 4.1,3 which shows the results of a simulation in which random samples were drawn again and again, to see how interval estimates behave. Suppose the population mean is zero and each vertical bar represents a different random sample and the resulting confidence interval. As you can see, most intervals overlap with the true population mean of zero (on the y axis), but we also expect one out of every 20 estimates (5%) to miss the mark (the bars shown in blue). In practice, we would normally only have one sample and wouldn’t know for sure if ours is one of the unlucky cases in which the confidence interval fails to include the population mean. What we do know is that we’ve followed a process that gives a correct answer 19 times out of 20.
What procedure is used to construct a confidence interval? We will learn the details in Chapter 6. For now, it is enough to know that there are well-established procedures for constructing confidence intervals in various settings. Even without knowing these exact procedures, you can hopefully begin to see the usefulness of confidence intervals from the examples in this chapter.
Note that confidence intervals can be computed for various parameters,4 not just the mean. In the following sections, we will see how confidence intervals can be applied to estimates of the difference in means as well as regression slope coefficients.
4.2.1 A Practical Example: Estimating the Difference in Means5
It is much more common for a researcher to be interested in the difference between means than in the specific values of the means themselves. Using statistical jargon introduced in the prior section, we could therefore say that the parameter of interest is often the difference in population means. We take as an example the data from the “Animal Research”6 case study. In this experiment, students rated (on a 7-point scale) whether they thought animal research is wrong. The sample sizes, means, and variances are shown separately for males and females in Table 4.1.
| Condition | n | Mean | Variance |
| Females | 17 | 5.353 | 2.743 |
| Males | 17 | 3.882 | 2.985 |
As you can see, the females rated animal research as more wrong than did the males. This sample difference between the female mean of 5.35 and the male mean of 3.88 is 1.47. However, the gender difference in this particular sample is not very important. What is important is the difference in the population. The difference in sample means is used to estimate the difference in population means. The accuracy of the estimate is revealed by a confidence interval.
In order to construct a confidence interval, we need to make some assumptions. The specifics might not make a lot of sense yet, but here are the three assumptions we need to make to obtain our confidence interval in this example:
The two populations have the same variance. This assumption is called the assumption of homogeneity of variance.
The populations are normally distributed.
Each value is sampled independently from each other value.
Using these assumptions, one can use a bunch of fancy math formulas (or statistical software) to get the following confidence interval:
\[ 0.29 \leq \mu_f - \mu_m \leq 2.65 \]
where \(\mu_f\) is the population mean for females and \(\mu_m\) is the population mean for males. Since the difference in these population means is the main parameter we wish to estimate, we could say the confidence interval for the parameter of interest is [0.29, 2.65]. Because all values within this range are positive, this analysis provides evidence that the mean for females is higher than the mean for males. More specifically, the difference between means in the population is likely to be between 0.29 and 2.65. Note that since 0 does not fall within the range of the confidence interval, this suggests that there is a difference between males and females, so we can also say that the results are statistically significant.
If, instead, we had found a confidence interval of [-1.03, 2.65], we could not rule out the possibility of no difference between males and females, since 0 falls between -1.03 and 2.65.
4.2.2 Introducing Confidence Intervals for Regression7
Let’s examine one more practical example of using confidence intervals, this time in the context of regression. For this example, we return to the regression results table presented at the end of the previous chapter (Section 3.5). The table is shown again here as Table 4.2.
| Coef. | Std. err. | p-value | |
|---|---|---|---|
| verb_sat | 0.0017 | 0.0010 | 0.10 |
| math_sat | 0.0048 | 0.0012 | 0.00014 |
| (intercept) | -0.91 | 0.42 | 0.033 |
| n | 105 | ||
| r^2 | 0.487 |
Because the coefficients we see in the table are just point estimates, confidence intervals can help us better understand the precision of these estimates by providing us with a range of plausible values for the coefficients. Notice that no confidence intervals have been provided in the table (which is a situation you may frequently encounter when reading social scientific research publications). Fortunately, we can easily calculate a good approximation of a confidence interval for a coefficient estimate \(\hat{\beta_i}\) as long as we also have its standard error estimate (\(s_{\beta_i}\)), which is provided in the table (in the column label “Std. err.”).8 We will learn exactly what a standard error is in Chapter 6, but for now, we can simply insert the standard error estimate into the following formulas:
\[ \text{Lower limit} \approx \hat{\beta_i} - 2\times s_{\beta_i} \]\[ \text{Upper limit} \approx \hat{\beta_i} + 2\times s_{\beta_i} \]
Note that these formulas are just an approximation; the formulas for precise intervals are shown in Section 6.3.3. In this approximation, all we are doing is multiplying the standard error by two to get the margin of error.9 From our initial point estimate of the slope, we can then add or subtract the margin of error to identify a full range of plausible values.
Our approximation approach provides an inexact but close approximation of a 95% confidence interval as long as the sample size is reasonably large (e.g., at least 30 more observations than the number of independent variables included in the regression). In this case, there are 105 observations and only two independent variables, so we will obtain a good approximation. And an approximation is usually the best we can hope for when calculating confidence intervals by hand from a regression table, since we will usually also lose some precision due to rounding error.
For the verbal SAT scores, we find the following limits:
\[ \text{Lower limit} \approx 0.0017 - (2)(0.0010) = -0.0003 \]\[ \text{Upper limit} \approx 0.0017 + (2)(0.0010) = 0.0037 \]
This is very close to the precise 95% confidence interval that one finds using statistical software to compute an exact interval: [-0.0003, 0.0038]. Any values within this range can be considered plausible values for the coefficient, according to our model results.
How do we interpret this confidence interval? Remember that when it comes to interpreting size, the coefficient indicates how many units the dependent variable is predicted to change when the independent variable increases by one unit. But with SAT scores, a 1-unit increase is so small that we found it more useful to consider a 100-point increase, which required multiplying the coefficient by 100. Doing so here, we can conclude that a 100-point increase in a student’s verbal SAT score (while assuming no change to the math SAT) predicts a change in the computer science GPA somewhere in the range of [-0.03, 0.38]. Zero is part of this range, so it’s entirely plausible that there is no association between verbal SAT score and computer science GPA (hence, the lack of statistical significance for this relationship). According to the model results, it is also plausible that a 100-point increase in verbal SAT is associated with the computer science GPA decreasing by as much as 0.03, or increasing by as much as 0.38. A 0.03 decrease in GPA is tiny, so we might feel comfortable ruling out the possibility that a good verbal SAT score has any substantial negative predictive effect for computer science GPA. But a positive effect of 0.38 grade points is much more substantial, so it is plausible that the verbal SAT has a meaningfully-large positive association with computer science GPA.
What about the math SAT? Using our approximation method:
\[ \text{Lower limit} \approx 0.0048 - (2)(0.0012) = 0.0024 \]\[ \text{Upper limit} \approx 0.0048 + (2)(0.0012) = 0.0072 \]
Multiplying these two values by 100, we find that a 100-point increase in one’s math SAT is plausibly associated with an increase of between 0.24 and 0.72 points on one’s computer science GPA.
4.2.3 Interpreting Confidence Intervals Correctly10
It is natural to interpret a 95% confidence interval as an interval with a 0.95 probability of containing the population mean. However, the proper interpretation is not that simple. One problem is that the computation of a confidence interval does not take into account any other information you might have about the value of the population mean. For example, if numerous prior studies had all found sample means above 110, it would not make sense to conclude that there is a 0.95 probability that the population mean is between 72.85 and 107.15, even if the sample you are currently analyzing yields this confidence interval.
So what is the correct interpretation? You can make the following statement any time you encounter a 95% confidence interval (of the form [A, B]):
Using a process with 95% accuracy (in theory), it is estimated that the parameter lies between A and B.
I realize this interpretation is a bit indirect; it is difficult to provide a technically-accurate and meaningful interpretation, despite the fact that confidence intervals have demonstrated great practical value.11 What makes their interpretation so difficult is the fact that the “% confidence” in a “95% confidence interval” refers to the accuracy of the process of creating a confidence interval—not the probability that a specific confidence interval we encounter will contain the true population parameter. If this distinction seems confusing, it is!
Fortunately, even if you miss the precise details, you will still probably get something useful out of confidence intervals.12 Nonetheless, let’s try to set the record straight.
An analogy may help. Suppose you are interacting with a chatbot that is truthful 95% of the time and lies the other 5%.13 For each statement, will you always conclude it has a 95% chance of being true? Not necessarily. If the chatbot discusses a topic you already know a lot about, you will probably be able to pick out the lies from the true statements with fairly high confidence. Some things the bot says will be things you know to be true, so you can be nearly 100% sure they are true. Other statements will be things you’re quite sure are wrong, so you will conclude that the probability they are true is close to 0%. If you wanted to be very systematic, you could even use the mathematical formula known as Bayes’ theorem14 to combine your prior knowledge of a statement’s probability of being true with the fact that a 95%-accurate bot claimed the statement was true, allowing you to precisely quantify how confident you should be about the statement’s truth in the end.
Now imagine you ask this same bot to start telling you about a topic you know nothing about. Absent any prior insights into which statements are likely to be true or false, it would now be reasonable to conclude that each statement the bot makes has a 95% chance of being true.
In the same way, it turns out that absent any other information, a 95% confidence interval is often a good approximation for a range of values that contains the population parameter with 95% probability.15 Thus, I think it is quite reasonable that many of us, when we see a mean estimate with a 95% confidence interval ranging from A to B, assume there is a 95% chance the population mean does indeed lie between A and B. But technically, that is not a direct interpretation of the confidence interval; instead, this statement about plausible values of the population mean is a subjective conclusion that I can draw based on the confidence interval. Another person might see the same confidence interval and reasonably decide—drawing on their own prior knowledge of the topic—that the confidence interval contains values that are highly implausible, and thus they would reach a different conclusion from me about how likely the interval is to contain the true population mean.
Building on the interpretation provided near the beginning of this section, if you want to elaborate on how the 95% confidence interval [A, B] can inform our practical understanding, you might add that:
Assuming no additional information and an appropriate statistical model, this result usually suggests that we can be about 95% confident the parameter lies between A and B.
This section is adapted from Mikki Hebl and David Lane. “Inferential Statistics.” Online Statistics Education: A Multimedia Course of Study. https://onlinestatbook.com/2/introduction/inferential.html↩︎
The beginning of this section is adapted from David M. Lane. “Confidence Intervals Introduction.” Online Statistics Education: A Multimedia Course of Study. https://onlinestatbook.com/2/estimation/confidence.html↩︎
This image is shared under CC-BY 4.0 and is adapted from Figure 1 of Nalborczyk, L., Bürkner, P. C., & Williams, D. R. (2019). Pragmatism should not be a substitute for statistical literacy, a commentary on Albers, Kiers, and van Ravenzwaaij (2018). Collabra: Psychology, 5(1), 13. https://doi.org/10.1525/collabra.197↩︎
A parameter is a value calculated in a population. For example, the mean of the numbers in a population is a parameter. Compare with a sample statistic, which is a value computed in a sample to estimate a parameter. (https://onlinestatbook.com/2/glossary/parameter.html)↩︎
This subsection is adapted from David M. Lane. “Difference between Means.” Online Statistics Education: A Multimedia Course of Study. https://onlinestatbook.com/2/estimation/difference_means.html↩︎
https://onlinestatbook.com/2/case_studies/animal_research.html↩︎
This subsection is written by Nathan Favero.↩︎
Some publications list t scores or z scores instead of standard errors. These t (or z) scores are typically just the coefficient divided by the standard error estimate, so you can obtain the standard error estimate by dividing the coefficient (\(\hat{\beta_i}\)) by its t score (\(t_{\beta_i}\)) as in the following formula: \(s_{\beta_i}=\hat{\beta_i}/t_{\beta_i}\).↩︎
Specifically, two is the approximate value by which the standard error should be multiplied, but a more exact value can be found using the t distribution, as explained in Section 6.3.↩︎
This subsection is mostly written by Nathan Favero, although the first paragraph is adapted from David M. Lane. “Confidence Intervals Introduction.” Online Statistics Education: A Multimedia Course of Study. https://onlinestatbook.com/2/estimation/confidence.html.↩︎
Stephens, M. (2023). The Bayesian lens and Bayesian blinkers. Philosophical Transactions of the Royal Society A, 381(2247), 20220144.
Kass, R. E. (2011). Statistical inference: The big picture. Statistical science: a review journal of the Institute of Mathematical Statistics, 26(1), 1.↩︎
Anderson, A. A. (2019). Assessing statistical results: magnitude, precision, and model uncertainty. The American Statistician, 73(sup1), 118-121.↩︎
This example is adapted from Behar, R., Grima, P., & Marco-Almagro, L. (2013). Twenty-five analogies for explaining statistical concepts. The American Statistician, 67(1), 44-48.↩︎
See https://onlinestatbook.com/2/glossary/bayes.html or https://onlinestatbook.com/2/probability/bayes_demo.html.↩︎
Kass, R. E. (2011). Statistical inference: The big picture. Statistical science: a review journal of the Institute of Mathematical Statistics, 26(1), 1.
Albers, C. J., Kiers, H. A., & van Ravenzwaaij, D. (2018). Credible confidence: A pragmatic view on the frequentist vs Bayesian debate. Collabra: Psychology, 4(1), 31.
Greenland, S., & Poole, C. (2013). Living with p values: resurrecting a Bayesian perspective on frequentist statistics. Epidemiology, 24(1), 62-68.↩︎