7 Hypothesis Testing
7.1 Introduction to Hypothesis Testing1
The statistician R. Fisher explained the concept of hypothesis testing with a story of a lady tasting tea. Here we will present an example based on James Bond who insisted that martinis should be shaken rather than stirred. Let’s consider a hypothetical experiment to determine whether Mr. Bond can tell the difference between a shaken and a stirred martini. Suppose we gave Mr. Bond a series of 16 taste tests. In each test, we flipped a fair coin to determine whether to stir or shake the martini. Then we presented the martini to Mr. Bond and asked him to decide whether it was shaken or stirred. Let’s say Mr. Bond was correct on 13 of the 16 taste tests. Does this prove that Mr. Bond has at least some ability to tell whether the martini was shaken or stirred?
This result does not prove that he does; it could be he was just lucky and guessed right 13 out of 16 times. But how plausible is the explanation that he was just lucky? To assess its plausibility, we determine the probability that someone who was just guessing would be correct 13/16 times or more. This probability can be computed from what is called the binomial distribution, and a binomial distribution calculator2 shows it to be 0.0106. This is a pretty low probability, and therefore someone would have to be very lucky to be correct 13 or more times out of 16 if they were just guessing. So either Mr. Bond was very lucky, or he can tell whether the drink was shaken or stirred. The hypothesis that he was guessing is not proven false, but considerable doubt is cast on it. Therefore, there is strong evidence that Mr. Bond can tell whether a drink was shaken or stirred.
Let’s consider another example. The case study Physicians’ Reactions3 sought to determine whether physicians spend less time with obese patients. Physicians were sampled randomly and each was shown a chart of a patient complaining of a migraine headache. They were then asked to estimate how long they would spend with the patient. The charts were identical except that for half the charts, the patient was obese and for the other half, the patient was of average weight. The chart a particular physician viewed was determined randomly. Thirty-three physicians viewed charts of average-weight patients and 38 physicians viewed charts of obese patients.
The mean time physicians reported that they would spend with obese patients was 24.7 minutes as compared to a mean of 31.4 minutes for average-weight patients. How might this difference between means have occurred? One possibility is that physicians were influenced by the weight of the patients. On the other hand, perhaps by chance, the physicians who viewed charts of the obese patients tend to see patients for less time than the other physicians. Random assignment of charts does not ensure that the groups will be equal in all respects other than the chart they viewed. In fact, it is certain the two groups differed in many ways by chance. The two groups could not have exactly the same mean age (if measured precisely enough such as in days). Perhaps a physician’s age affects how long physicians see patients. There are innumerable differences between the groups that could affect how long they view patients. With this in mind, is it plausible that these chance differences are responsible for the difference in times?
To assess the plausibility of the hypothesis that the difference in mean times is due to chance, we compute the probability of getting a difference as large or larger than the observed difference (31.4 - 24.7 = 6.7 minutes) if the difference were, in fact, due solely to chance. Using methods presented in Chapter 8, this probability can be computed to be 0.0057. Since this is such a low probability, we have confidence that the difference in times is due to the patient’s weight and is not due to chance.
7.1.1 The Probability Value
It is very important to understand precisely what the probability values mean. In the James Bond example, the computed probability of 0.0106 is the probability he would be correct on 13 or more taste tests (out of 16) if he were just guessing.
It is easy to mistake this probability of 0.0106 as the probability he cannot tell the difference. This is not at all what it means.
The probability of 0.0106 is the probability of a certain outcome (13 or more out of 16) assuming a certain state of the world (James Bond was only guessing). It is not the probability that a state of the world is true. Although this might seem like a distinction without a difference, consider the following example. An animal trainer claims that a trained bird can determine whether or not numbers are evenly divisible by 7. In an experiment assessing this claim, the bird is given a series of 16 test trials. On each trial, a number is displayed on a screen and the bird pecks at one of two keys to indicate its choice. The numbers are chosen in such a way that the probability of any number being evenly divisible by 7 is 0.50. The bird is correct on 9/16 choices. Using the binomial calculator, we can compute that the probability of being correct nine or more times out of 16 if one is only guessing is 0.40. Since a bird who is only guessing would do this well 40% of the time, these data do not provide convincing evidence that the bird can tell the difference between the two types of numbers. As a scientist, you would be very skeptical that the bird had this ability. Would you conclude that there is a 0.40 probability that the bird can tell the difference? Certainly not! You would think the probability is much lower than 0.0001.
To reiterate, the probability value (p value) is the probability of an outcome (9/16 or better) and not the probability of a particular state of the world (the bird was only guessing). In statistics, it is conventional to refer to possible states of the world as hypotheses since they are hypothesized states of the world. Using this terminology, the probability value is the probability of an outcome given the hypothesis. It is not the probability of the hypothesis given the outcome.
This is not to say that we ignore the probability of the hypothesis. If the probability of the outcome given the hypothesis is sufficiently low, we have evidence that the hypothesis is false. However, we do not compute the probability that the hypothesis is false. In the James Bond example, the hypothesis is that he cannot tell the difference between shaken and stirred martinis. The probability value is low (0.0106), thus providing evidence that he can tell the difference. However, we have not computed the probability that he can tell the difference. A branch of statistics called Bayesian statistics provides methods for computing the probabilities of hypotheses. These computations require that one specify the probability of the hypothesis before the data are considered and, therefore, are difficult to apply in some contexts.
7.1.2 The Null Hypothesis
The hypothesis that an apparent effect is due to chance is called the null hypothesis. In the Physicians’ Reactions example, the null hypothesis is that in the population of physicians, the mean time expected to be spent with obese patients is equal to the mean time expected to be spent with average-weight patients. This null hypothesis can be written as:
\[ \mu_{obese} = \mu_{average} \]
or as
\[ \mu_{obese} - \mu_{average} = 0. \]
The null hypothesis in a correlational study of the relationship between high school grades and college grades would typically be that the population correlation is 0. This can be written as
\[ \rho = 0 \]
where \(\rho\) is the population correlation (not to be confused with r, the correlation in the sample).
Although the null hypothesis is usually that the value of a population parameter is 0, there are occasions in which the null hypothesis is a value other than 0. For example, if one were testing whether a subject differed from chance in their ability to determine whether a flipped coin would come up heads or tails, the null hypothesis would be that \(\pi\) = 0.5.
Keep in mind that the null hypothesis is typically the opposite of the researcher’s hypothesis. In the Physicians’ Reactions study, the researchers hypothesized that physicians would expect to spend less time with obese patients. The null hypothesis that the two types of patients are treated identically is put forward with the hope that it can be discredited and therefore rejected. If the null hypothesis were true, a difference as large or larger than the sample difference of 6.7 minutes would be very unlikely to occur. Therefore, the researchers rejected the null hypothesis of no difference and concluded that in the population, physicians intend to spend less time with obese patients.
If the null hypothesis is rejected, then the alternative to the null hypothesis (called the alternative hypothesis) is accepted. The alternative hypothesis is simply the reverse of the null hypothesis. If the null hypothesis
\[ \mu_{obese} = \mu_{average} \]
is rejected, then there are two alternatives:
\[ \mu_{obese} < \mu_{average} \]
\[ \mu_{obese} > \mu_{average} \]
Naturally, the direction of the sample means determines which alternative is adopted. Some textbooks have incorrectly argued that rejecting the null hypothesis that two population means are equal does not justify a conclusion about which population mean is larger. Kaiser (1960)4 showed how it is justified to draw a conclusion about the direction of the difference.
7.2 Steps in Hypothesis Testing5
There’s much to learn about hypothesis testing, but before going any further, here’s an overview of the four basic steps of any hypothesis test. Some of the details won’t make sense yet, but we’ll explain them in more detail in the following sections.
The first step is to specify the null hypothesis. For a two-tailed test, the null hypothesis is typically that a parameter equals zero although there are exceptions. A typical null hypothesis is \(\mu_1 - \mu_2 = 0\) which is equivalent to \(\mu_1 = \mu_2\). For a one-tailed test, the null hypothesis is either that a parameter is greater than or equal to zero or that a parameter is less than or equal to zero. If the prediction is that \(\mu_1\) is larger than \(\mu_2\), then the null hypothesis (the reverse of the prediction) is \(\mu_2 - \mu_1 \geq 0\). This is equivalent to \(\mu_1 \leq \mu_2\).
The second step is to specify the \(\alpha\) level which is also known as the significance level. Typical values are 0.05 and 0.01.
The third step is to compute the probability value (also known as the p value). This is the probability of obtaining a sample statistic as different or more different from the parameter specified in the null hypothesis given that the null hypothesis is true.
Finally, compare the probability value with the \(\alpha\) level. If the probability value is lower then you reject the null hypothesis. Keep in mind that rejecting the null hypothesis is not an all-or-none decision. The lower the probability value, the more confidence you can have that the null hypothesis is false. However, if your probability value is higher than the conventional \(\alpha\) level of 0.05, most scientists will consider your findings inconclusive. Failure to reject the null hypothesis does not constitute support for the null hypothesis. It just means you do not have sufficiently strong data to reject it.
7.3 One- and Two-Tailed Tests6
In the James Bond case study,7 Mr. Bond was given 16 trials on which he judged whether a martini had been shaken or stirred. He was correct on 13 of the trials. From the binomial distribution, we know that the probability of being correct 13 or more times out of 16 if one is only guessing is 0.0106. Figure 7.1 shows a graph of the binomial distribution. The red bars show the values greater than or equal to 13. As you can see in the figure, the probabilities are calculated for the upper tail of the distribution. A probability calculated in only one tail of the distribution is called a “one-tailed probability.”
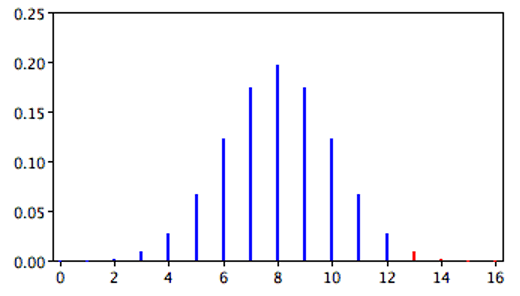
A slightly different question can be asked of the data: “What is the probability of getting a result as extreme or more extreme than the one observed?” Since the chance expectation is 8/16, a result of 3/16 is equally as extreme as 13/16. Thus, to calculate this probability, we would consider both tails of the distribution. Since the binomial distribution is symmetric when \(\pi\) = 0.5, this probability is exactly double the probability of 0.0106 computed previously. Therefore, p = 0.0212. A probability calculated in both tails of a distribution is called a “two-tailed probability” (see Figure 7.2).
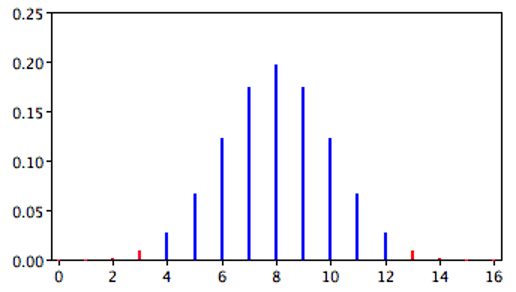
Should the one-tailed or the two-tailed probability be used to assess Mr. Bond’s performance? That depends on the way the question is posed. If we are asking whether Mr. Bond can tell the difference between shaken or stirred martinis, then we would conclude he could if he performed either much better than chance or much worse than chance. If he performed much worse than chance, we would conclude that he can tell the difference, but he does not know which is which. Therefore, since we are going to reject the null hypothesis if Mr. Bond does either very well or very poorly, we will use a two-tailed probability.
On the other hand, if our question is whether Mr. Bond is better than chance at determining whether a martini is shaken or stirred, we would use a one-tailed probability. What would the one-tailed probability be if Mr. Bond were correct on only 3 of the 16 trials? Since the one-tailed probability is the probability of the right-hand tail, it would be the probability of getting 3 or more correct out of 16. This is a very high probability and the null hypothesis would not be rejected.
The null hypothesis for the two-tailed test is \(\pi = 0.5\). By contrast, the null hypothesis for the one-tailed test is \(\pi \leq 0.5\).8 Accordingly, we reject the two-tailed hypothesis if the sample proportion deviates greatly from 0.5 in either direction. The one-tailed hypothesis is rejected only if the sample proportion is much greater than 0.5. The alternative hypothesis in the two-tailed test is \(\pi \ne 0.5\). In the one-tailed test it is \(\pi > 0.5\).
You should always decide whether you are going to use a one-tailed or a two-tailed probability before looking at the data. Statistical tests that compute one-tailed probabilities are called one-tailed tests; those that compute two-tailed probabilities are called two-tailed tests. Two-tailed tests are much more common than one-tailed tests in scientific research because an outcome signifying that something other than chance is operating is usually worth noting. One-tailed tests are appropriate when it is not important to distinguish between no effect and an effect in the unexpected direction. For example, consider an experiment designed to test the efficacy of a treatment for the common cold. The researcher would only be interested in whether the treatment was better than a placebo control. It would not be worth distinguishing between the case in which the treatment was worse than a placebo and the case in which it was the same because in both cases the drug would be worthless.
Some have argued that a one-tailed test is justified whenever the researcher predicts the direction of an effect. The problem with this argument is that if the effect comes out strongly in the non-predicted direction, the researcher is not justified (according to the test) in concluding that the effect is not zero. Since this is unrealistic, one-tailed tests are usually viewed skeptically if justified on this basis alone.
7.4 Significance Testing9
A low probability value casts doubt on the null hypothesis. How low must the probability value be in order to conclude that the null hypothesis is false? Although there is clearly no right or wrong answer to this question, it is conventional to conclude the null hypothesis is false if the probability value is less than 0.05. More conservative researchers conclude the null hypothesis is false only if the probability value is less than 0.01. When a researcher concludes that the null hypothesis is false, the researcher is said to have rejected the null hypothesis. The probability value below which the null hypothesis is rejected is called the \(\alpha\) (alpha) level or simply \(\alpha\). It is also called the significance level.
When the null hypothesis is rejected, the effect is said to be statistically significant. For example, in the Physicians’ Reactions case study,10 the probability value is 0.0057. Therefore, the effect of obesity is statistically significant and the null hypothesis that obesity makes no difference is rejected. It is very important to keep in mind that statistical significance means only that the null hypothesis of exactly no effect is rejected; it does not mean that the effect is important, which is what “significant” usually means in contexts outside of statistics. When an effect is statistically significant, you can have confidence the effect is not exactly zero. Finding that an effect is significant does not tell you about how large or important the effect is.
Do not confuse statistical significance with practical significance. A small effect can be highly significant if the sample size is large enough.
Why does the word “significant” in the phrase “statistically significant” mean something so different from other uses of the word? Interestingly, this is because the meaning of “significant” in everyday language has changed. It turns out that when the procedures for hypothesis testing were developed, something was “significant” if it signified something. Thus, finding that an effect is statistically significant signifies that the effect is real and not due to chance. Over the years, the meaning of “significant” changed, leading to the potential misinterpretation.
There are two approaches (at least) to conducting significance tests. In one (favored by R. Fisher), a significance test is conducted and the probability value reflects the strength of the evidence against the null hypothesis.11 If the probability is below 0.01, the data provide strong evidence that the null hypothesis is false. If the probability value is below 0.05 but larger than 0.01, then the null hypothesis is typically rejected, but not with as much confidence as it would be if the probability value were below 0.01. Probability values between 0.05 and 0.10 provide weak evidence against the null hypothesis and, by convention, are not considered low enough to justify rejecting it. Higher probabilities provide less evidence that the null hypothesis is false.
The alternative approach (favored by the statisticians Neyman and Pearson) is to specify an \(\alpha\) level before analyzing the data. If the data analysis results in a probability value below the \(\alpha\) level, then the null hypothesis is rejected; if it is not, then the null hypothesis is not rejected. According to this perspective, if a result is significant, then it does not matter how significant it is. Moreover, if it is not significant, then it does not matter how close to being significant it is. Therefore, if the 0.05 level is being used, then probability values of 0.049 and 0.001 are treated identically. Similarly, probability values of 0.06 and 0.34 are treated identically.
The former approach (preferred by Fisher) is more suitable for scientific research and will be adopted here. The latter is more suitable for applications in which a yes/no decision must be made. For example, if a statistical analysis were undertaken to determine whether a machine in a manufacturing plant were malfunctioning, the statistical analysis would be used to determine whether or not the machine should be shut down for repair. The plant manager would be less interested in assessing the weight of the evidence than knowing what action should be taken. There is no need for an immediate decision in scientific research where a researcher may conclude that there is some evidence against the null hypothesis, but that more research is needed before a definitive conclusion can be drawn.
7.5 Testing a Single Mean12
The way we calculate the probability (\(p\)) value for a hypothesis test depends on what type of statement is made in our null hypothesis. Normally, statistical software will automatically compute a p value behind the scenes, but we still want to learn a bit about how the software comes up with this value. To illustrate what these calculations can look like, this section will focus on what to do if we want to test a null hypothesis stating that the population mean is equal to some hypothesized value. For example, suppose an experimenter wanted to know if people are influenced by a subliminal message and performed the following experiment. Each of nine subjects is presented with a series of 100 pairs of pictures, and for each pair they are asked to select one. As a pair of pictures is presented, a subliminal message is presented suggesting the picture that the subject should choose. The question is whether the (population) mean number of times the suggested picture is chosen is equal to 50 (the number we would expect if subliminal messages have no effect). In other words, the null hypothesis is that the population mean (\(\mu\)) is 50. The (hypothetical) data are shown in Table 7.1. The data in Table 7.1 have a sample mean (\(\bar{X}\)) of 51. Thus the sample mean differs from the hypothesized population mean by 1.
| Frequency |
|---|
| 45 |
| 48 |
| 49 |
| 49 |
| 51 |
| 52 |
| 53 |
| 55 |
| 57 |
The significance test consists of computing the probability of a sample mean differing from \(\mu\) by one (the difference between the hypothesized population mean and the sample mean) or more. The first step is to determine the sampling distribution of the mean. As we learned in the prior chapter, the mean and standard deviation of the sampling distribution of the mean are
\[ \mu_{\bar{X}} = \mu \]
and
\[ \sigma_{\bar{X}} = \frac{\sigma}{\sqrt{n}} \]
respectively. It is clear that if the null hypothesis is true, \(\mu_{\bar{X}}\) = 50. In order to compute the standard deviation of the sampling distribution of the mean, we have to know the population standard deviation (\(\sigma\)).
The current example was constructed to be one of the few instances in which the standard deviation is known. In practice, it is very unlikely that you would know \(\sigma\) and therefore you would use \(s\), the sample estimate of \(\sigma\). However, it is instructive to see how the probability is computed if \(\sigma\) is known before proceeding to see how it is calculated when \(\sigma\) is estimated.
For the current example, if the null hypothesis is true, then based on a well-established formula for the binomial distribution, one can compute that the variance of the number correct is
\[ \sigma^2 = N \pi (1-\pi) = 100(0.5)(1-0.5) = 25 \]
where \(N\) is the number of times a subject makes a selection between two pictures. Therefore, \(\sigma\) = 5 (since \(\sigma = \sqrt{\sigma^2}=\sqrt{25}=5\)). For a \(\sigma\) of 5 and an \(n\) of 9, the standard deviation of the sampling distribution of the mean is \(5/\sqrt{9} = 1.667\). Recall that the standard deviation of a sampling distribution is called the standard error.
To recap, we wish to know the probability of obtaining a sample mean of 51 or greater assuming the null hypothesis is true. If the null hypothesis is true, the sampling distribution of the mean has a mean of 50 and a standard deviation of 1.667. To compute the relevant probability, we will make the assumption that the sampling distribution of the mean is normally distributed. We can then use a normal distribution calculator as shown in Figure 7.3.
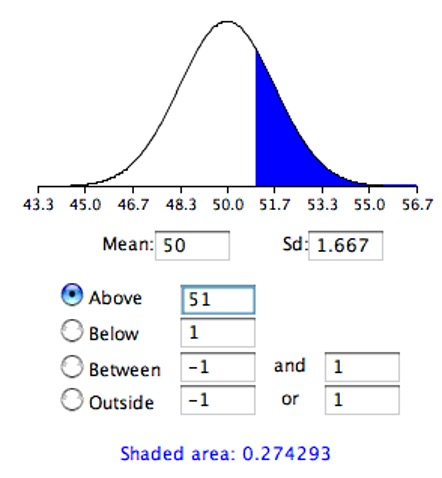
Notice that the mean is set to 50, the standard deviation to 1.667, and the area above 51 is requested and shown to be 0.274.
Therefore, the probability of obtaining a sample mean of 51 or larger is 0.274. Since a mean of 51 or higher is not unlikely under the assumption that the subliminal message has no effect, the effect is not significant and the null hypothesis is not rejected.
The test conducted above was a one-tailed test because it computed the probability of a sample mean being one or more points higher than the hypothesized mean of 50 and the area computed was the area above 51. To test the two-tailed hypothesis, you would compute the probability of a sample mean differing by one or more in either direction from the hypothesized mean of 50. You would do so by computing the probability of a mean being less than or equal to 49 or greater than or equal to 51.
The results from a normal distribution calculator are shown in Figure 7.4.
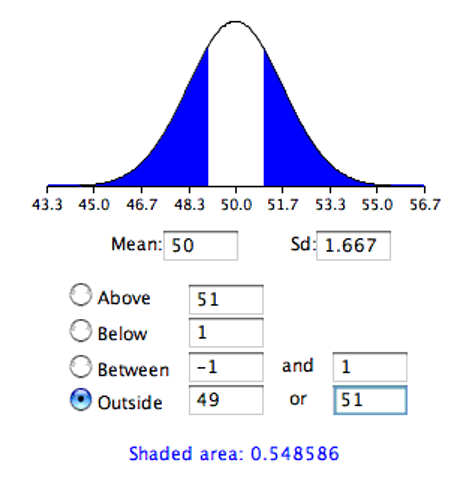
As you can see, the probability is 0.548 which, as expected, is twice the probability of 0.274 shown in Figure 7.3.
Before normal calculators such as the one illustrated above were widely available, probability calculations were made based on the standard normal distribution. This was done by computing \(Z\) based on the formula
\[ Z = \frac{\bar{X}-\mu_0}{\sigma_{\bar{X}}} \]
where \(Z\) is the value on the standard normal distribution, \(\bar{X}\) is the sample mean, \(\mu_0\) is the hypothesized value of the mean (under the null hypothesis),13 and \(\sigma_{\bar{X}}\) is the standard error of the mean. For this example, \(Z\) = (51-50)/1.667 = 0.60. Use a normal calculator, with a mean of 0 and a standard deviation of 1, as shown below.
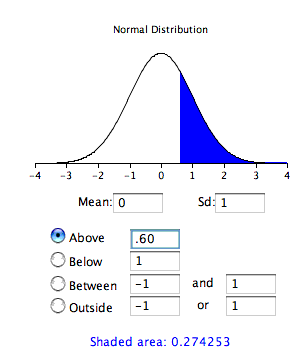
Notice that the probability (the shaded area) is the same as previously calculated (for the one-tailed test).
As noted, in real-world data analyses it is very rare that you would know \(\sigma\) and wish to estimate \(\mu\). Typically \(\sigma\) is not known and is estimated in a sample by s, and \(\sigma_{\bar{X}}\) is estimated by \(s_{\bar{X}}\). For our next example, we will consider the data in the “ADHD Treatment” case study.14 These data consist of the scores of 24 children with ADHD on a delay of gratification (DOG) task. Each child was tested under four dosage levels. Table 7.2 shows the data for the placebo (0 mg) and highest dosage level (0.6 mg) of methylphenidate. Of particular interest here is the column labeled “Diff” that shows the difference in performance between the 0.6 mg (D60) and the 0 mg (D0) conditions. These difference scores are positive for children who performed better in the 0.6 mg condition than in the control condition and negative for those who scored better in the control condition. If methylphenidate has a positive effect, then the mean difference score in the population will be positive. The null hypothesis is that the mean difference score in the population is 0.
| D0 | D60 | Diff | ||||
|---|---|---|---|---|---|---|
| 57 | 62 | 5 | ||||
| 27 | 49 | 22 | ||||
| 32 | 30 | -2 | ||||
| 31 | 34 | 3 | ||||
| 34 | 38 | 4 | ||||
| 38 | 36 | -2 | ||||
| 71 | 77 | 6 | ||||
| 33 | 51 | 18 | ||||
| 34 | 45 | 11 | ||||
| 53 | 42 | -11 | ||||
| 36 | 43 | 7 | ||||
| 42 | 57 | 15 | ||||
| 26 | 36 | 10 | ||||
| 52 | 58 | 6 | ||||
| 36 | 35 | -1 | ||||
| 55 | 60 | 5 | ||||
| 36 | 33 | -3 | ||||
| 42 | 49 | 7 | ||||
| 36 | 33 | -3 | ||||
| 54 | 59 | 5 | ||||
| 34 | 35 | 1 | ||||
| 29 | 37 | 8 | ||||
| 33 | 45 | 12 | ||||
| 33 | 29 | -4 |
To test this null hypothesis, we compute what we call a t statistic (as opposed to a z statistic) because we will compare this value to the t distribution—a distribution which allows for accurate inferences when \(\sigma\) is estimated rather than known (see Section 6.3.2). We compute t using a special case of the following formula:
\[ \text{t} = \frac{\text{statistic} -\text{hypothesized value}}{\text{estimated standard error of the statistic}} \]
The special case of this formula applicable to testing a single mean is
\[ \text{t} = \frac{\bar{X}-\mu_0}{s_{\bar{X}}} \]
where \(t\) is the value we compute for the significance test, \(\bar{X}\) is the sample mean, \(\mu_0\) is the hypothesized value of the population mean, and \(s_{\bar{X}}\) is the estimated standard error of the mean. Notice the similarity of this formula to the formula for \(Z\) we saw before.
In the previous example, we assumed that the scores were normally distributed. In this case, it is the population of difference scores that we assume to be normally distributed.
The mean (\(\bar{X}\)) of the n = 24 difference scores is 4.958, the hypothesized value of \(\mu\) is 0, and the standard deviation (s) is 7.538. The estimate of the standard error of the mean is computed as:
\[ s_{\bar{X}} = \frac{s}{\sqrt{n}} = \frac{7.5382}{\sqrt{24}} = 1.54 \]
Therefore, t = 4.96/1.54 = 3.22. The probability value for t depends on the degrees of freedom. The number of degrees of freedom is equal to n - 1 = 23. As shown below, a t distribution calculator finds that the probability of a t less than -3.22 or greater than 3.22 is only 0.0038. Therefore, if the drug had no effect, the probability of finding a difference between means as large or larger (in either direction) than the difference found is very low. Therefore the null hypothesis that the population mean difference score is zero can be rejected. The conclusion is that the population mean for the drug condition is higher than the population mean for the placebo condition.
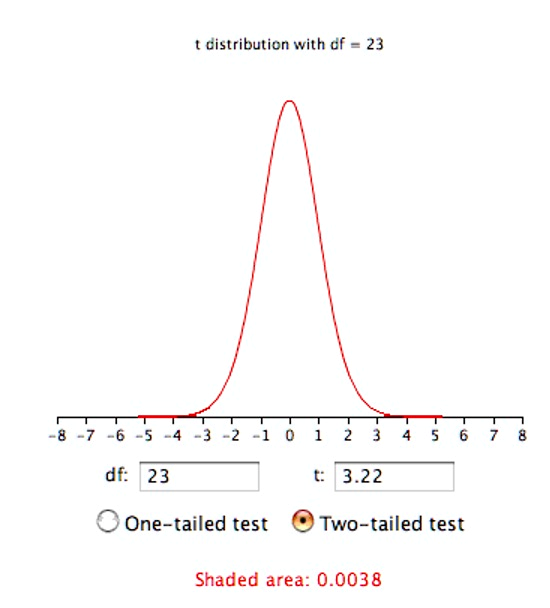
In order to conduct this hypothesis test, we made the following assumptions:
Each value is sampled independently from each other value.
The values are sampled from a normal distribution.
Now that we’ve filled in more of the details of hypothesis tests, you may want to go back and review Section 7.2 to see whether you can follow the succinct overview of the hypothesis testing approach. Once you can follow that description, it is a good indication that you have understood the key concepts essential to every hypothesis test.
7.6 Type I and Type II Errors15
In the Physicians’ Reactions case study,16 the probability value associated with the significance test is 0.0057. Therefore, the null hypothesis was rejected, and it was concluded that physicians intend to spend less time with obese patients. Despite the low probability value, it is possible that the null hypothesis of no true difference between obese and average-weight patients is true and that the large difference between sample means occurred by chance. If this is the case, then the conclusion that physicians intend to spend less time with obese patients is in error. This type of error is called a Type I error. More generally, a Type I error occurs when a significance test results in the rejection of a true null hypothesis.
By one common convention, if the probability value is below 0.05, then the null hypothesis is rejected. Another convention, although slightly less common, is to reject the null hypothesis if the probability value is below 0.01. The threshold for rejecting the null hypothesis is called the \(\alpha\) (alpha) level or simply \(\alpha\). It is also called the significance level. As discussed in the section on significance testing, it is better to interpret the probability value as an indication of the weight of evidence against the null hypothesis than as part of a decision rule for making a reject or do-not-reject decision. Therefore, keep in mind that rejecting the null hypothesis is not an all-or-nothing decision.
The Type I error rate is affected by the \(\alpha\) level: the lower the \(\alpha\) level, the lower the Type I error rate. It might seem that \(\alpha\) is the probability of a Type I error. However, this is not correct. Instead, \(\alpha\) is the probability of a Type I error given that the null hypothesis is true. If the null hypothesis is false, then it is impossible to make a Type I error.
The second type of error that can be made in significance testing is failing to reject a false null hypothesis. This kind of error is called a Type II error. Unlike a Type I error, a Type II error is not really an error. When a statistical test is not significant, it means that the data do not provide strong evidence that the null hypothesis is false. Lack of significance does not support the conclusion that the null hypothesis is true. Therefore, a researcher should not make the mistake of incorrectly concluding that the null hypothesis is true when a statistical test was not significant. Instead, the researcher should consider the test inconclusive. Contrast this with a Type I error in which the researcher erroneously concludes that the null hypothesis is false when, in fact, it is true.
A Type II error can only occur if the null hypothesis is false. If the null hypothesis is false, then the probability of a Type II error is called \(\beta\) (beta). The value of this probability \(\beta\) will be affected by the sample size (larger sample sizes make it less likely a false null hypothesis will fail to be rejected), but the exact formula for calculating \(\beta\) depends on the particular type of hypothesis test being conducted. The probability of correctly rejecting a false null hypothesis equals \(1- \beta\) and is called statistical power. When researchers say that a study is “well-powered,” they mean that the sample size is large enough to reject a false null hypothesis with fairly high probability under certain assumptions (such as a reasonably large effect size).
7.7 Significance Test for a Regression Slope Coefficient17
To conclude this chapter, let’s briefly revisit the very first type of hypothesis test we encountered in this textbook (though we did not call it that at the time): testing for the significance of a regression slope coefficient (Section 3.5). Now that we know more about hypothesis testing, let’s fill in some of the details of how to calculate the p-values we rely upon to determine the significance of these coefficients.
The appropriate type of significance test in the case of the regression coefficients we have learn about is a t test. Recall the general formula for a t test:
\[ t = \frac{\text{statistic - hypothesized value}}{\text{estimated standard error of the statistic}} \]
As applied to the case of the slope in a simple regression, the statistic is the sample value of the slope coefficient (\(\hat{\beta}\)). Generally, the hypothesized value is 0, meaning that we want to test a null hypothesis of no relationship between the independent and dependent variables.
Just as when we generated a confidence interval for the slope coefficient in Section 6.3.3, the degrees of freedom for this t test is n-2. We also use the same calculation for the estimated standard error as when calculating a confidence interval, so refer back to Chapter 6 (specifically Appendix II) if you would like to review how we calculate it.
With the data example we used when learning precise confidence interval calculations (Section 6.3.3), we had a sample slope coefficient (\(\hat{\beta}\)) of 0.425, a standard error (\(s_{\beta}\)) of 0.305, and a sample size of 5. Given these numbers and a hypothesized value of 0:
\[ t = \frac{0.425-0}{0.305} = 1.39 \] \[ df = n-2 = 5-2 = 3. \]
With these values of \(t\) and \(df\), the p value for a two-tailed t test is 0.26. Therefore, the slope is not significantly different from 0 under this example.
This section is adapted from David M. Lane. “Introduction.” Online Statistics Education: A Multimedia Course of Study. https://onlinestatbook.com/2/logic_of_hypothesis_testing/intro.html↩︎
https://onlinestatbook.com/2/calculators/binomial_dist.html↩︎
Kaiser, H. F. (1960) Directional statistical decisions. Psychological Review, 67, 160-167.↩︎
This section is adapted from David M. Lane. “Steps in Hypothesis Testing.” Online Statistics Education: A Multimedia Course of Study. https://onlinestatbook.com/2/logic_of_hypothesis_testing/steps.html↩︎
This section is adapted from David M. Lane. “One- and Two-Tailed Tests.” Online Statistics Education: A Multimedia Course of Study. https://onlinestatbook.com/2/logic_of_hypothesis_testing/tails.html↩︎
Some sources write the null hypothesis of the one-tailed test identically to the two-tailed test (\(\pi = 0.5\)). While this alternative notation does not preserve the intuitive logic of the null hypothesis being the strict reverse of the alternative hypothesis, it does hint at how the p-value in a one-tailed test is calculated, since a distribution with \(\pi = 0.5\) is used to determine the p-value (as shown in Figure 7.1).↩︎
This section is adapted from David M. Lane. “Significance Testing.” Online Statistics Education: A Multimedia Course of Study. https://onlinestatbook.com/2/logic_of_hypothesis_testing/significance.html↩︎
See also: Goodman, W. M., Spruill, S. E., & Komaroff, E. (2019). A proposed hybrid effect size plus p-value criterion: empirical evidence supporting its use. The American Statistician, 73(sup1), 168-185.↩︎
This section is adapted from David M. Lane. “Testing a Single Mean.” Online Statistics Education: A Multimedia Course of Study. https://onlinestatbook.com/2/tests_of_means/single_mean.html↩︎
The subscript \(_0\) in \(\mu_0\) (the population mean according to the null hypothesis) corresponds to how we typically represent the null hypothesis: \(H_0\).↩︎
This section is adapted from David M. Lane. “Type I and Type II Errors.” Online Statistics Education: A Multimedia Course of Study. https://onlinestatbook.com/2/logic_of_hypothesis_testing/errors.html↩︎
This section is adapted from David M. Lane. “Inferential Statistics for b and r.” Online Statistics Education: A Multimedia Course of Study. https://onlinestatbook.com/2/regression/inferent↩︎