8 Comparing Means (How a Qualitative Variable Relates to a Quantitative One)
It is much more common for a researcher to be interested in the difference between means—the focus of this chapter—than in the specific values of the means themselves. Note that we already learned in the chapter on graphing how to visually depict a comparison of means/medians using boxplots (Section 1.4.2). The formal analyses described in this chapter pair well with that sort of graph, since the formal tests allow one to make statements that explicitly account for the uncertainty and imprecision inherent in statistical inference.
8.1 Difference between Two Means1
This section covers how to test for differences between means from two separate groups of subjects, using an independent-groups t test.
We take as an example the data from the “Animal Research” case study, previously described when discussing confidence intervals (Section 4.2.1).2 As a reminder, students rated (on a 7-point scale) whether they thought animal research is wrong.
| Group | n | Mean | Variance | |||||
|---|---|---|---|---|---|---|---|---|
| Females | 17 | 5.353 | 2.743 | |||||
| Males | 17 | 3.882 | 2.985 |
As we noted previously, the female mean is 1.47 units higher than the male mean (Table 8.1). This is just the difference in our sample, however, and we wish to draw an inference about the difference in the population means.
In order to test whether there is a difference between population means, we are going to make three assumptions (just as we did when constructing a confidence interval):
The two populations have the same variance. This assumption is called the assumption of homogeneity of variance.
The populations are normally distributed.
Each value is sampled independently3 from each other value. This assumption requires that each subject provide only one value. If a subject provides two scores, then the scores are not independent.
One could look at these assumptions in much more detail, but suffice it to say that small-to-moderate violations of assumptions 1 and 2 do not make much difference. It is important not to violate assumption 3.
In practice, most researchers use software to automate calculation with all formulas we encounter in this chapter. Nonetheless, your ability to understand the output of the software may improve if you have some idea of what’s happening under the hood. As we saw in the previous chapter, the following general formula is used for significance testing based on the t distribution:
\[ \text{t} = \frac{\text{statistic} - \text{hypothesized value}}{\text{estimated standard error of the statistic}} \]
In this case, our statistic is the difference between sample means and our hypothesized value is 0 because the null hypothesis states that the difference between population means is 0.
We continue to use the data from the “Animal Research” case study and will compute a significance test on the difference between the mean score of the females and the mean score of the males.
The first step is to compute the statistic, which is simply the difference between means.
\[ \bar{X}_1 - \bar{X}_2 = 5.3529 - 3.8824 = 1.4705 \]
Since the hypothesized value is 0, we do not need to subtract it from the statistic.
The next step is to compute the estimate of the standard error of the statistic. In this case, the statistic is the difference between means, so the estimated standard error of the statistic is \(s_{\text{diff}}\) (which can also be written as \(s_{\bar{X}_1 - \bar{X}_2}\)). The formula for the standard error of the difference between means is:4
\[ \sigma_{\text{diff}} = \sqrt{\frac{\sigma^2_1}{n_1}+\frac{\sigma^2_2}{n_2}} = \sqrt{\frac{\sigma^2}{n}+\frac{\sigma^2}{n}} = \sqrt{\frac{2\sigma^2}{n}} \]
where \(\sigma^2_1\) and \(n_1\) are the variance and sample size of the first group, and \(\sigma^2_2\) and \(n_2\) are the variance and sample size of the second group. Note that since we assumed \(\sigma^2_1 = \sigma^2_2\) (as our first of the three assumptions listed above), we can represent both of these variances as simply \(\sigma^2\). Likewise, when \(n_1\) = \(n_2\) (as in our example with equal numbers of females and males), it is conventional to use “\(n\)” to refer to the sample size of each group.
Because the value of \(\sigma^2\) is unknown, we estimate it by averaging our two sample variances, relying again on our assumption that the two population variances are the same (and thus each sample’s variance should be an equally valid estimate of \(\sigma^2\)). This estimate of variance is can be written as follows:
\[ \text{MSE}= \frac{s^2_1+s^2_2}{2} \]
where MSE is our estimate of \(\sigma^2\). In this example,
\[ \text{MSE} = (2.743 + 2.985)/2 = 2.864. \]
We can now estimate \(\sigma_{\text{diff}}\) with \(s_{\text{diff}}\), substituting in MSE where we previously saw \(\sigma^2\) in the formula for \(\sigma_{\text{diff}}\). Since n (the number of scores in each group) is 17,
\[ s_{\text{diff}} = \sqrt{\frac{2MSE}{n}} = \sqrt{\frac{(2)(2.864)}{17}} = 0.5805. \]
The next step is to compute t by plugging these values into the formula:
\[ t = \frac{1.4705}{0.5805} = 2.533. \]
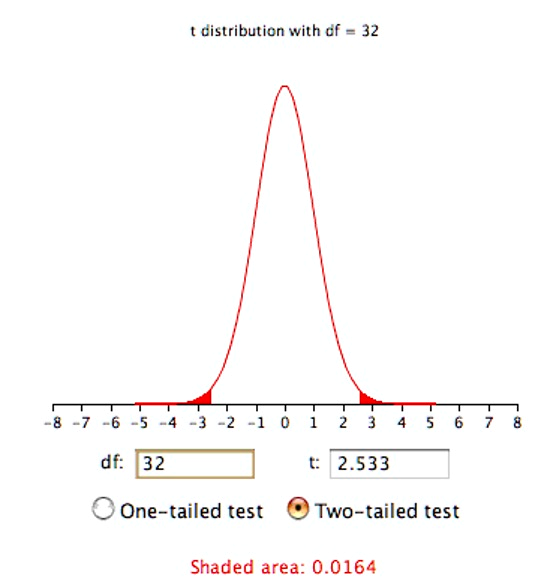
Finally, we compute the probability of getting a \(t\) as large or larger than 2.533 or as small or smaller than -2.533. To do this, we need to know the degrees of freedom. The degrees of freedom is the number of independent estimates of variance on which \(MSE\) is based. This is equal to (\(n_1\) - 1) + (\(n_2\) - 1), and for this example, \(n_1\) = \(n_2\) = 17. Therefore, the degrees of freedom is 16 + 16 = 32.
Once we have the degrees of freedom, we can use a t distribution calculator5 to find the probability. Figure 8.1 shows that the probability value (p) for a two-tailed test is 0.0164. The two-tailed test is used when the null hypothesis can be rejected regardless of the direction of the effect. As shown in Figure 8.1, it is the probability of a t < -2.533 or a t > 2.533.
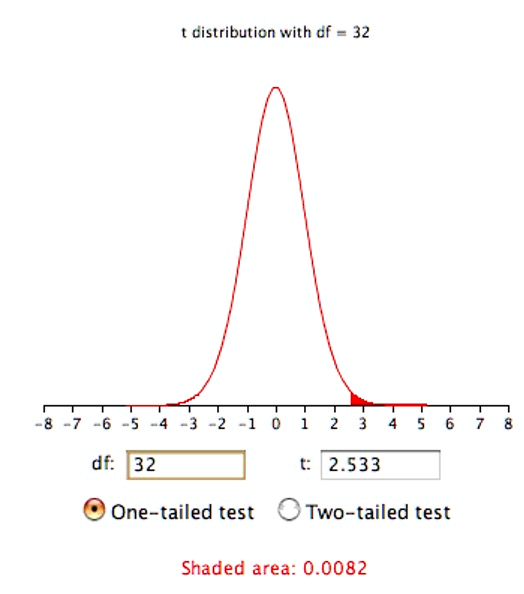
The results of a one-tailed test are shown in Figure 8.2. As you can see, the probability value of 0.0082 is half the value for the two-tailed test.
8.1.1 Formatting Data for Computer Analysis
Most computer programs that compute t tests require your data to be in a specific form. Consider the data in Table 8.2.
| Group 1 | Group 2 | |||
|---|---|---|---|---|
| 3 | 2 | |||
| 4 | 6 | |||
| 5 | 8 |
Here there are two groups, each with three observations. To format these data for a computer program, you normally have to use two variables: the first specifies the group the subject is in and the second is the score itself. The reformatted version of the data in Table 8.2 is shown in Table 8.3. We sometimes describe the original format as “wide” form and the reformatted data as “long” form.
| Group | Y | |||
|---|---|---|---|---|
| 1 | 3 | |||
| 1 | 4 | |||
| 1 | 5 | |||
| 2 | 2 | |||
| 2 | 6 | |||
| 2 | 8 |
Using statistical software, we’d find that the t value is -0.718, the df = 4, and p = 0.512.
8.2 Pairwise Comparisons Among Multiple Means6
Many experiments are designed to compare more than two conditions. We will take as an example the case study “Smiles and Leniency.”7 In this study, the effect of different smiles on the leniency shown to a person was investigated. Four different types of smiles (neutral, false, felt, and miserable) were shown. “Type of Smile” is the independent variable, and the dependent variable is a leniency rating given by the subject to a fictional student (depicted with one of the four smiles) in an academic misconduct case. An obvious way to proceed would be to do a t test of the difference between each group mean and each of the other group means. This procedure would lead to the six comparisons shown in Table 8.4.
| false vs. felt |  |
 |
| false vs. miserable |  |
 |
| false vs. neutral |  |
 |
| felt vs. miserable |  |
 |
| felt vs. neutral |  |
 |
| miserable vs. neutral |  |
 |
The problem with this approach is that if you did this analysis, you would have six chances to make a Type I error. Therefore, if you were using the 0.05 significance level, the probability that you would make a Type I error on at least one of these comparisons is greater than 0.05.8 The more means that are compared, the more the Type I error rate is inflated. Figure 8.3 shows the number of possible comparisons between pairs of means (pairwise comparisons) as a function of the number of means. If there are only two means, then only one comparison can be made. If there are 12 means, then there are 66 possible comparisons.
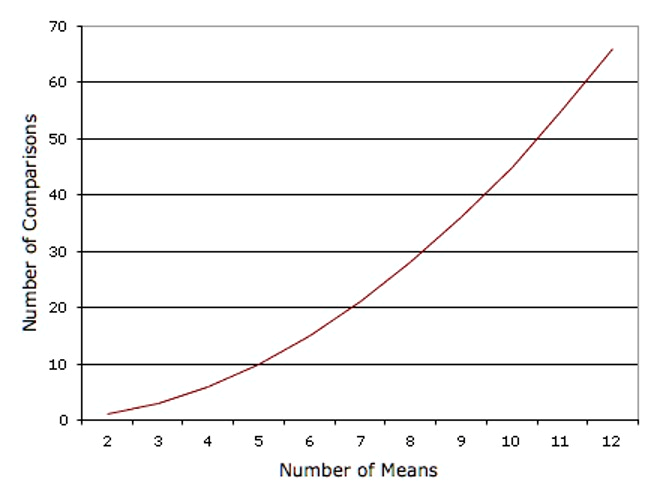
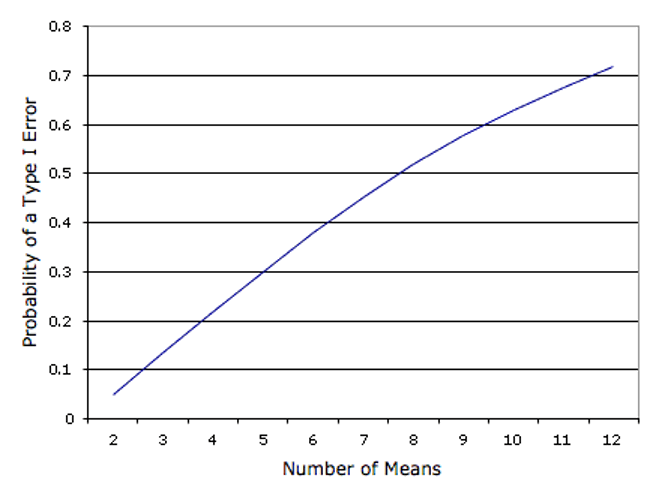
Figure 8.4 shows the probability of a Type I error as a function of the number of means. As you can see, if you have an experiment with 12 means, the probability is about 0.70 that at least one of the 66 comparisons among means would be significant even if all 12 population means were the same.
The Type I error rate can be controlled using a test called the Tukey Honestly Significant Difference test or Tukey HSD for short. The Tukey HSD test is one example of a multiple comparison test, but several alternatives are frequently used, such as the Bonferroni correction. Regardless of the exact method used for a multiple comparison test, the interpretation of results is similar. The Tukey HSD is based on a variation of the t distribution that takes into account the number of means being compared. This distribution is called the studentized range distribution.
Normally, statistical software will make all the necessary calculations for you in the background. But to illustrate what sorts of calculations the software is relying on, let’s return to the leniency study to see how to compute the Tukey HSD test. You will see that the computations are very similar to those of an independent-groups t test. The steps are outlined below:
- Compute the means and variances of each group. For our example, they are shown in Table 8.5.
| Condition | Mean | Variance | ||||
|---|---|---|---|---|---|---|
| False | 5.37 | 3.34 | ||||
| Felt | 4.91 | 2.83 | ||||
| Miserable | 4.91 | 2.11 | ||||
| Neutral | 4.12 | 2.32 |
Compute MSE, which is simply the mean of the variances. It is equal to 2.65.
Compute Q (using the formula below) for each pair of means, where \(\bar{X}_i\) is one mean, \(\bar{X}_j\) is the other mean, and \(n\) is the number of scores in each group. For these data, there are 34 observations per group. The value in the denominator is 0.279. \[ Q=\frac{\bar{X}_i-\bar{X}_j}{\sqrt{\frac{MSE}{n}}} \]
Compute p for each comparison using a Studentized Range Calculator.9 The degrees of freedom is equal to the total number of observations minus the number of means. For this experiment, df = 136 - 4 = 132.
The tests for these data are shown in Table 8.6.
| Comparison | \(\bar{X}_i - \bar{X}_j\) | \(Q\) | \(p\) |
|---|---|---|---|
| False - Felt | 0.46 | 1.65 | 0.649 |
| False - Miserable | 0.46 | 1.65 | 0.649 |
| False - Neutral | 1.25 | 4.48 | 0.010 |
| Felt - Miserable | 0.00 | 0.00 | 1.000 |
| Felt - Neutral | 0.79 | 2.83 | 0.193 |
| Miserable - Neutral | 0.79 | 2.83 | 0.193 |
The only significant comparison is between the false smile and the neutral smile.
It is not unusual to obtain results that on the surface appear paradoxical. For example, these results appear to indicate that (a) the false smile is the same as the miserable smile, (b) the miserable smile is the same as the neutral control, and (c) the false smile is different from the neutral control. This apparent contradiction is avoided if you are careful not to accept the null hypothesis when you fail to reject it. The finding that the false smile is not significantly different from the miserable smile does not mean that they are really the same. Rather it means that there is not convincing evidence that they are different. Similarly, the non-significant difference between the miserable smile and the control does not mean that they are the same. The proper conclusion is that the false smile is higher than the control and that the miserable smile is either (a) equal to the false smile, (b) equal to the control, or (c) somewhere in-between.
The assumptions of the Tukey test are essentially the same as for an independent-groups t test: normality, homogeneity of variance, and independent observations. The test is quite robust to violations of normality. Violating homogeneity of variance can be more problematical than in the two-sample case since the MSE is based on data from all groups. The assumption of independence of observations is important and should not be violated.
8.2.1 Computer Analysis
For most computer programs, you should format your data the same way you do for an independent-groups t test. The only difference is that if you have, say, four groups, you would code each group as 1, 2, 3, or 4 rather than just 1 or 2.
8.2.2 Tukey’s Test Need Not be a Follow-Up to ANOVA
Some textbooks introduce the Tukey test only as a follow-up to an analysis of variance (ANOVA), a technique introduced in the following section. There is no logical or statistical reason why you should not use the Tukey test even if you do not compute an ANOVA (or even know what one is). If you or your instructor do not wish to take our word for this, see the excellent article on this and other issues in statistical analysis by Leland Wilkinson and the APA Board of Scientific Affairs’ Task Force on Statistical Inference, published in the American Psychologist, August 1999, Vol. 54, No. 8, 594–604.
8.3 Analysis of Variance (ANOVA)
8.3.1 Introduction10
Analysis of Variance (ANOVA) is a statistical method used to test differences between two or more means. It may seem odd that the technique is called “Analysis of Variance” rather than “Analysis of Means.” The name is appropriate because inferences about means are made by analyzing variance, as outlined in this chapter’s appendix.
ANOVA is used to test general rather than specific differences among means. This can be seen best by example, so we will continue considering the data on leniency and smiles we examined in the prior section on the Tukey HSD test.
ANOVA tests the non-specific null hypothesis that all four population means are equal. That is,
\[ \mu_{false} = \mu_{felt} = \mu_{miserable} = \mu_{neutral} \]
in our example. More generally, the null hypothesis tested by ANOVA is that the population means for all conditions are the same. For whatever data is being examined, this can be written as:
\[ H_0: \mu_1 = \mu_2 = ... = \mu_k \]
where \(H_0\) is the null hypothesis and k is the number of conditions (k = 4 in our example).
This non-specific null hypothesis is sometimes called the omnibus null hypothesis. When the omnibus null hypothesis is rejected, the conclusion is that at least one population mean is different from at least one other mean. However, since the ANOVA does not reveal which means are different from which, it offers less specific information than the Tukey HSD test. The Tukey HSD is therefore preferable to ANOVA in this situation.
You might be wondering why you should learn about ANOVA when the Tukey test is better. One reason is that there are complex types of analyses that can be done with ANOVA and not with the Tukey test. A second is that ANOVA is one of the most commonly-used technique for comparing means, and it is important to understand ANOVA in order to understand research reports.
8.3.2 The Critical Step: Calculating an F Ratio11
There are many types of ANOVA, but for our example, we will use what is called a one-factor between-subjects design. Other types of ANOVA are beyond the scope of what is covered in this text.
More details are provided in this chapter’s appendix, but the critical step in an ANOVA is comparing what is called the mean square error (MSE) to the mean square between (MSB). MSB estimates a larger quantity than MSE only when the population means are not equal, so finding a larger MSB than an MSE is a sign that the population means are not equal. But since MSB could be larger than MSE by chance even if the population means are equal, MSB must be much larger than MSE in order to justify the conclusion that the population means differ. But how much larger must MSB be? For the “Smiles and Leniency” data, the MSB and MSE are 9.179 and 2.649, respectively. Is that difference big enough? To answer, we would need to know the probability of getting that big a difference or a bigger difference if the population means were all equal. The mathematics necessary to answer this question were worked out by the statistician R. Fisher. Although Fisher’s original formulation took a slightly different form, the standard method for determining the probability is based on the ratio of MSB to MSE. This ratio is named after Fisher and is called the F ratio.
For these data, the F ratio is
\[ F = \frac{9.179}{2.649} = 3.465. \]
Therefore, the MSB is 3.465 times higher than MSE. Would this have been likely to happen if all the population means were equal? That depends on the sample size. With a small sample size, it would not be too surprising because results from small samples are unstable. However, with a very large sample, the MSB and MSE are almost always about the same (assuming the null hypothesis is true), and an F ratio of 3.465 or larger would be very unusual. Figure 8.5 shows the sampling distribution of F for the sample size in the “Smiles and Leniency” study. As you can see, it has a positive skew.
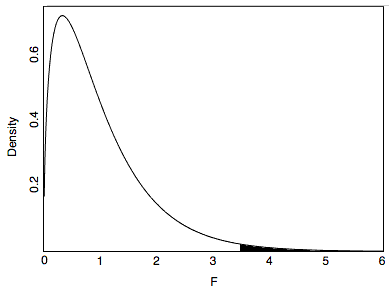
From Figure 8.5, you can see that F ratios of 3.465 or above are unusual occurrences. The area to the right of 3.465 represents the probability of an F that large or larger and is equal to 0.018. In other words, given the null hypothesis that all the population means are equal, the probability value (p) is 0.018 and therefore the null hypothesis can be rejected. The conclusion that at least one of the population means is different from at least one of the others is justified.
The shape of the F distribution depends on the sample size. More precisely, it depends on two degrees of freedom (df) parameters: one for the numerator (MSB) and one for the denominator (MSE). Recall that the degrees of freedom for an estimate of variance is equal to the number of observations minus one. Since the MSB is the variance of k means (where k is the number of groups), it has k - 1 df. The MSE is an average of k variances, each with n - 1 df. Therefore, the df for MSE is k(n - 1) = N - k, where N is the total number of observations, n is the number of observations in each group, and k is the number of groups. To summarize:
\[ df_{\text{numerator}} = k-1 \]\[ df_{\text{denominator}} = N-k \]
For the “Smiles and Leniency” data,
\[ df_{\text{numerator}} = k-1 = 4-1 = 3 \]\[ df_{\text{denominator}} = N-k = 136-4 = 132 \]\[ F = 3.465 \]
An F distribution calculator12 shows that p = 0.018. Again, because this value is less than 0.05, one would generally reject the null hypothesis and conclude that average leniency varies depending on type of smile. The p-value from an ANOVA is sometimes reported in a larger table of summary results such as Table 8.7.
| Source | df | SSQ | MS | F | p |
|---|---|---|---|---|---|
| Condition | 3 | 27.5349 | 9.1783 | 3.465 | 0.0182 |
| Error | 132 | 349.6544 | 2.6489 | ||
| Total | 135 | 377.1893 |
8.3.3 Relationship to T Tests and Regression
Since an ANOVA and an independent-groups t test can both test the difference between two means, you might be wondering which one to use. Fortunately, it does not matter since the results will always be the same. When there are only two groups, the following relationship between F and t will always hold:
\[ F(1,dfd) = t^2(df) \]
where dfd is the degrees of freedom for the denominator of the F test and df is the degrees of freedom for the t test. dfd will always equal df. And because of how their probability distributions are constructed, these values of F and t will yield identical p-values for the (two tailed) null hypothesis of no difference between the two means.
There is also a third equivalent way to compare two means: using regression, as described in Chapter 12. More generally, regression and ANOVA are two sides of the same coin and will yield equivalent results (assuming the same data/assumptions), even when testing for differences among more than two means. Statistical software will generally include a model F statistic among the results shown for a regression, and in the case of a model a single qualitative independent variable, the regression model F statistic will be the same F ratio used in an ANOVA. Because of this equivalence, whether one reports results as an ANOVA or regression is usually a matter of habit and familiarity. In some social science literatures, ANOVA results are rarely reported because researchers typically default to using regression instead.
8.4 Appendix: More about ANOVA
Terminology for Various Designs13
There are many types of experimental designs that can be analyzed by ANOVA. This section discusses many of these designs and defines several key terms used.
Factors and Levels
In describing an ANOVA design, the term factor is a synonym of independent variable. Therefore, in the case study “Smiles and Leniency,” “Type of Smile” is the factor in this experiment. Since four types of smiles were compared, the factor “Type of Smile” has four levels.
An ANOVA conducted on a design in which there is only one factor is called a one-way ANOVA. If an experiment has two factors, then the ANOVA is called a two-way ANOVA. For example, suppose an experiment on the effects of age and gender on reading speed were conducted using three age groups (8 years, 10 years, and 12 years) and the two genders (male and female). The factors would be age and gender. Age would have three levels and gender would have two levels.
Between- and Within-Subjects Factors
In the “Smiles and Leniency” study, the four levels of the factor “Type of Smile” were represented by four separate groups of subjects. When different subjects are used for the levels of a factor, the factor is called a between-subjects factor or a between-subjects variable. The term “between subjects” reflects the fact that comparisons are between different groups of subjects.
In the “ADHD Treatment” study,14 in which every subject was tested with each of four dosage levels (0, 0.15, 0.30, 0.60 mg/kg) of a drug. Therefore there was only one group of subjects, and comparisons were not between different groups of subjects but between conditions within the same subjects. When the same subjects are used for the levels of a factor, the factor is called a within-subjects factor or a within-subjects variable. Within-subjects variables are sometimes referred to as repeated-measures variables since there are repeated measurements of the same subjects.
Multi-Factor Designs
It is common for designs to have more than one factor. For example, consider a hypothetical study of the effects of age and gender on reading speed in which males and females from the age levels of 8 years, 10 years, and 12 years are tested. There would be a total of six different groups as shown in Table 8.8.
| Group | Gender | Age |
|---|---|---|
| 1 | Female | 8 |
| 2 | Female | 10 |
| 3 | Female | 12 |
| 4 | Male | 8 |
| 5 | Male | 10 |
| 6 | Male | 12 |
This design has two factors: age and gender. Age has three levels and gender has two levels. When all combinations of the levels are included (as they are here), the design is called a factorial design. A concise way of describing this design is as a Gender (2) x Age (3) factorial design where the numbers in parentheses indicate the number of levels. Complex designs frequently have more than two factors and may have combinations of between- and within-subjects factors.
Details of One-Factor ANOVA (Between Subjects)15
This section shows how ANOVA can be used to analyze a one-factor between-subjects design.
Analysis of variance is a method for testing differences among means by analyzing variance. The test is based on two estimates of the population variance (\(\sigma^2\)). One estimate is called the mean square error (MSE) and is based on differences among scores within the groups. MSE estimates \(\sigma^2\) regardless of whether the null hypothesis is true (the population means are equal). The second estimate is called the mean square between (MSB) and is based on differences among the sample means. MSB only estimates \(\sigma^2\) if the population means are equal. If the population means are not equal, then MSB estimates a quantity larger than \(\sigma^2\). Therefore, if the MSB is much larger than the MSE, then the population means are unlikely to be equal. On the other hand, if the MSB is about the same as MSE, then the data are consistent with the null hypothesis that the population means are equal.
Before proceeding with the calculation of MSE and MSB, it is important to consider the assumptions made by ANOVA:
The populations have the same variance. This assumption is called the assumption of homogeneity of variance.
The populations are normally distributed.
Each value is sampled independently from each other value. This assumption requires that each subject provide only one value. If a subject provides two scores, then the values are not independent; to accomodate such data, one must use within-subjects ANOVA (a type of ANOVA which is easily implemented but which lies beyond the scope of this text).
These assumptions are the same as for a t test of differences between groups (Section 8.1) except that they apply to two or more groups, not just to two groups.
Sample Sizes
As in the main part of the chapter, we will use as our example the “Smiles and Leniency” case study. The first calculations in this section all assume that there is an equal number of observations in each group (unequal sample size calculations are shown later in this appendix). We will refer to the number of observations in each group as n and the total number of observations as N. For these data there are four groups of 34 observations. Therefore, n = 34 and N = 136.
Computing MSE
Recall that the assumption of homogeneity of variance states that the variance within each of the populations (\(\sigma^2\)) is the same. This variance, \(\sigma^2\), is the quantity estimated by MSE and is computed as the mean of the sample variances. For these data, the MSE is equal to 2.6489.
Computing MSB
The formula for MSB is based on the fact that the variance of the sampling distribution of the mean is
\[ \sigma^2_\mu = \frac{\sigma^2}{n} \]
where n is the sample size of each group. Rearranging this formula, we have
\[ \sigma^2 = n\sigma^2_\mu. \]
Therefore, if we knew the variance of the sampling distribution of the mean, we could compute \(\sigma^2\) by multiplying it by n. Although we do not know the variance of the sampling distribution of the mean, we can estimate it with the variance of the sample means. For the leniency data, the variance of the four sample means is 0.270. To estimate \(\sigma^2\), we multiply the variance of the sample means (0.270) by n (the number of observations in each group, which is 34). We find that MSB = 9.179.
To sum up these steps:
Compute the means.
Compute the variance of the means.
Multiply the variance of the means by n.
Recap
If the population means are equal, then both MSE and MSB are estimates of \(\sigma^2\) and should therefore be about the same. Naturally, they will not be exactly the same since they are just estimates and are based on different aspects of the data: The MSB is computed from the sample means and the MSE is computed from the sample variances.
If the population means are not equal, then MSE will still estimate \(\sigma^2\) because differences in population means do not affect variances. However, differences in population means affect MSB since differences among population means are associated with differences among sample means. It follows that the larger the differences among sample means, the larger the MSB. In short, MSE estimates \(\sigma^2\) whether or not the population means are equal, whereas MSB estimates \(\sigma^2\) only when the population means are equal and estimates a larger quantity when they are not equal.
As shown in Section 8.3.2, we compare the MSE to the MSB by way of an F ratio in order to determine a p-value for the null hypothesis that the population means are all equal.
One-Tailed or Two?
Is the probability value from an F ratio a one-tailed or a two-tailed probability? In the literal sense, it is a one-tailed probability since, as you could see in Figure 8.5 earlier in the chapter, the probability is the area in the right-hand tail of the distribution. However, the F ratio is sensitive to any pattern of differences among means. It is, therefore, a test of a two-tailed hypothesis and is best considered a two-tailed test.
Sources of Variation
Why do scores in an experiment differ from one another? Consider the scores of two subjects in the “Smiles and Leniency” study: one from the “False Smile” condition and one from the “Felt Smile” condition. An obvious possible reason that the scores could differ is that the subjects were treated differently (they were in different conditions and saw different stimuli). A second reason is that the two subjects may have differed with regard to their tendency to judge people leniently. A third is that, perhaps, one of the subjects was in a bad mood after receiving a low grade on a test. You can imagine that there are innumerable other reasons why the scores of the two subjects could differ. All of these reasons except the first (subjects were treated differently) are possibilities that were not under experimental investigation and, therefore, all of the differences (variation) due to these possibilities are unexplained. It is traditional to call unexplained variance error even though there is no implication that an error was made. Therefore, the variation in this experiment can be thought of as being either variation due to the condition the subject was in or due to error (the sum total of all reasons the subjects’ scores could differ that were not measured).
One of the important characteristics of ANOVA is that it partitions the variation into its various sources. In ANOVA, the term sum of squares (SSQ) is used to indicate variation. The total variation is defined as the sum of squared differences between each score and the mean of all subjects. The mean of all subjects is called the grand mean and is designated as GM. (When there is an equal number of subjects in each condition, the grand mean is the mean of the condition means.) The total sum of squares is defined as
\[ SSQ_\text{total} = \sum(X - GM)^2 \]
which means to take each score, subtract the grand mean from it, square the difference, and then sum up these squared values. For the “Smiles and Leniency” study, \(\text{SSQ}_\text{total} = 377.19\).
The sum of squares condition is calculated as shown below.
\[ SSQ_\text{condition} = n \left[ (\bar{X}_1 - GM)^2 + (\bar{X}_2 - GM)^2 + ... +(\bar{X}_k - GM)^2 \right] \]
where n is the number of scores in each group, k is the number of groups, \(\bar{X}_1\) is the mean for Condition 1, \(\bar{X}_2\) is the mean for Condition 2, and \(\bar{X}_k\) is the mean for Condition k. For the Smiles and Leniency study, the values are:
\[ SSQ_\text{condition} = 34 \left[ (5.37-4.83)^2 + (4.91-4.83)^2 + (4.91-4.83)^2 +(4.12-4.83)^2 \right] \]\[ = 27.5 \]
If there are unequal sample sizes, the only change is that the following formula is used for the sum of squares condition:
\[ SSQ_\text{condition} = n_1 (\bar{X}_1 - GM)^2 + n_2 (\bar{X}_2 - GM)^2 + ... + n_k (\bar{X}_k - GM)^2 \]
where \(n_i\) is the sample size of the \(i\)th condition. \(\text{SSQ}_\text{total}\) is computed the same way as shown above.
The sum of squares error is the sum of the squared deviations of each score from its group mean. This can be written as
\[ SSQ_\text{error} = \sum(X_{i1} - \bar{X}_1)^2 + \sum(X_{i2} - \bar{X}_2)^2 + ...+ \sum(X_{ik} - \bar{X}_k)^2. \]
where \(X_{i1}\) is the \(i\)th score in group 1 and \(\bar{X}_1\) is the mean for group 1, \(X_{i2}\) is the \(i\)th score in group 2 and \(\bar{X}_2\) is the mean for group 2, etc. For the “Smiles and Leniency” study, the means are: 5.368, 4.912, 4.912, and 4.118. The \(SSQ_\text{error}\) is therefore:
\[ (2.5-5.368)^2 + (5.5-5.368)^2 + ... + (6.5-4.118)^2 = 349.65 \]
The sum of squares error can also be computed by subtraction:
\[ SSQ_\text{error} = SSQ_\text{totoal} - SSQ_\text{condition} \]\[ SSQ_\text{error} = 377.189 - 27.535 = 349.65 \]
Therefore, the total sum of squares of 377.19 can be partitioned into \(SSQ_\text{condition}\) (27.53) and \(SSQ_\text{error}\) (349.66).
Once the sums of squares have been computed, the mean squares (MSB and MSE) can be computed easily. The formulas are:
\[ MSB = \frac{SSQ_\text{condition}}{dfn} \]
where dfn is the degrees of freedom numerator and is equal to k - 1 = 3.
\[ MSB = \frac{27.535}{3} = 9.18 \]
which is the same value of MSB obtained previously (except for rounding error). Similarly,
\[ MSE = \frac{SSQ_\text{error}}{dfd} \]
where dfd is the degrees of freedom for the denominator and is equal to N - k.
\[ dfd = 136 - 4 = 132 \]\[ MSE = 349.66/132 = 2.65 \]
which is the same as obtained previously (except for rounding error). Note that the dfd is often called the dfe for degrees of freedom error.
As we saw in the main portion of the chapter, SSQ and MSB/MSE can be reported alongside the F statistic and p-value for an ANOVA in a results table (Table 8.7). Since most people conducting ANOVA these days do so with automated computer software, you will likely see a results table along these lines in whatever software you use if you conduct ANOVA yourself.
Formatting Data for Computer Analysis
Most computer programs that compute ANOVAs require your data to be in a specific form. Consider the data in Table 8.9.
| Group 1 | Group 2 | Group 3 |
|---|---|---|
| 3 | 2 | 8 |
| 4 | 4 | 5 |
| 5 | 6 | 5 |
Here there are three groups, each with three observations. To format these data for a computer program, you normally have to use two variables: the first specifies the group the subject is in and the second is the score itself. The reformatted version of the data in Table 8.9 is shown in Table 8.10.
| Group | Y |
|---|---|
| 1 | 3 |
| 1 | 4 |
| 1 | 5 |
| 2 | 2 |
| 2 | 4 |
| 2 | 6 |
| 3 | 8 |
| 3 | 5 |
| 3 | 5 |
This section is adapted from David M. Lane. “Difference between Two Means (Independent Groups).” Online Statistics Education: A Multimedia Course of Study. https://onlinestatbook.com/2/tests_of_means/difference_means.html↩︎
https://onlinestatbook.com/2/case_studies/animal_research.html↩︎
Two variables are said to be independent if the value of one variable provides no information about the value of the other variable. In this case, if knowing the value of the X variable for one observation could help us predict the value of X for another observation, the two values of X are not independent. For example, if there is clustered sampling, such that selecting an individual into the sample implies that neighbors with similar X values are also likely to be in the sample, the observations are not independent.↩︎
For a more detailed discussion, see https://onlinestatbook.com/2/sampling_distributions/samplingdist_diff_means.html↩︎
This section is adapted from David M. Lane. “All Pairwise Comparisons Among Means.” Online Statistics Education: A Multimedia Course of Study. https://onlinestatbook.com/2/tests_of_means/pairwise.html↩︎
When discussing probability of Type I errors, we assume all null hypotheses are true, since a Type I error can’t occur if the null hypothesis is false.↩︎
https://onlinestatbook.com/2/calculators/studentized_range_dist.html↩︎
This subsection is adapted from David M. Lane. “Introduction.” Online Statistics Education: A Multimedia Course of Study. https://onlinestatbook.com/2/analysis_of_variance/intro.html↩︎
This subsection and the following are adapted from David M. Lane. “One-Factor ANOVA (Between Subjects).” Online Statistics Education: A Multimedia Course of Study. https://onlinestatbook.com/2/analysis_of_variance/one-way.html↩︎
This subsection is adapted from David M. Lane. “Analysis of Variance Designs.” Online Statistics Education: A Multimedia Course of Study. https://onlinestatbook.com/2/analysis_of_variance/anova_designs.html↩︎
This subsection is adapted from David M. Lane. “One-Factor ANOVA (Between Subjects).” Online Statistics Education: A Multimedia Course of Study. https://onlinestatbook.com/2/analysis_of_variance/one-way.html↩︎